![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Binomi- ja
multinomikertoimet [ 1 2 3 4 ]
Binomi- ja
multinomikertoimet [ 1 2 3 4 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) polynomit,
polynomit, ![[#]](kuvat/msam10-c-4.gif) lukumäärän laskeminen
lukumäärän laskeminen
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Binomi- ja
multinomikertoimet [ 1 2 3 4 ] Binomi- ja
multinomikertoimet [ 1 2 3 4 ]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) polynomit, polynomit, ![[#]](kuvat/msam10-c-4.gif) lukumäärän laskeminen lukumäärän laskeminen
|
|
n ensimmäisen luonnollisen luvun tulo on n-kertoma; tätä merkitään huutomerkin avulla:
n! = 1 . 2 . 3 . ... . n.
Lisäksi asetetaan 0! = 1.
Esimerkiksi 6! = 1 . 2 . 3 . 4 . 5 . 6 = 720.
Kertomafunktio f : 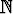

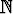 , f(n) = n! kasvaa erittäin nopeasti argumentin n
kasvaessa. Esimerkiksi
, f(n) = n! kasvaa erittäin nopeasti argumentin n
kasvaessa. Esimerkiksi
40! = 815915283247897734345611269596115894272000000000,
missä on 48 numeroa; 100! on suuruusluokaltaan 10158.
Suuria kertomia voidaan arvioida Stirlingin kaavalla:
n! 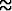 nne-n
nne-n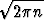 .
.
(James Stirling oli englantilaissyntyinen Venetsiassa toiminut professori, joka julkaisi kaavan vuonna 1730.)
Kertomafunktion yleistyksenä on gammafunktio 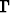 (x), joka positiivisilla
reaaliarvoilla x määritellään integraalilla
(x), joka positiivisilla
reaaliarvoilla x määritellään integraalilla
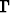 (x) =
(x) = 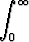 e-ttx-1 dt
e-ttx-1 dt
ja jolle pätee n! = 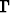 (n + 1), missä n on luonnollinen luku.
(n + 1), missä n on luonnollinen luku.
![[#]](kuvat/msam10-c-4.gif) luonnollinen luku luonnollinen luku![[#]](kuvat/msam10-c-4.gif) funktio funktio![[#]](kuvat/msam10-c-4.gif) funktio (reaali-) funktio (reaali-)![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12