Stokastinen muuttuja
Otosavaruudessa 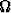 määritelty funktio on stokastinen muuttuja eli satunnaismuuttuja.
Yleensä tämä on reaaliarvoinen.
määritelty funktio on stokastinen muuttuja eli satunnaismuuttuja.
Yleensä tämä on reaaliarvoinen.
Kahta noppaa heitettäessä otosavaruus 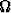 muodostuu pareista (m, n), missä m ja
n ovat heiton tuloksena saadut silmäluvut, ts. m ja n saavat toisistaan riippumatta
arvot 1, 2, 3, 4, 5, 6. Esimerkki stokastisesta muuttujasta on näiden summa:
X(m, n) = m + n. Stokastinen muuttuja (siis funktio) X saa tällöin äärellisen
monta arvoa: 2, 3, ..., 12.
muodostuu pareista (m, n), missä m ja
n ovat heiton tuloksena saadut silmäluvut, ts. m ja n saavat toisistaan riippumatta
arvot 1, 2, 3, 4, 5, 6. Esimerkki stokastisesta muuttujasta on näiden summa:
X(m, n) = m + n. Stokastinen muuttuja (siis funktio) X saa tällöin äärellisen
monta arvoa: 2, 3, ..., 12.
Heitettäessä tikkaa tauluun voidaan otosavaruudeksi 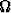 ottaa xy-taso, jonka origo
sijaitsee taulun keskipisteessä. Alkeistapaukset eli otosavaruuden alkiot
muodostuvat koordinaattipareista (x, y), jotka kuvaavat tikan osumiskohtaa. Eräs
stokastinen muuttuja on osumiskohdan etäisyys taulun keskipisteestä:
D(x, y) =
ottaa xy-taso, jonka origo
sijaitsee taulun keskipisteessä. Alkeistapaukset eli otosavaruuden alkiot
muodostuvat koordinaattipareista (x, y), jotka kuvaavat tikan osumiskohtaa. Eräs
stokastinen muuttuja on osumiskohdan etäisyys taulun keskipisteestä:
D(x, y) = 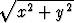 . Muuttujan D arvoja ovat kaikki ei-negatiiviset reaaliluvut.
. Muuttujan D arvoja ovat kaikki ei-negatiiviset reaaliluvut.
Edellisessä esimerkissä on kyseessä diskreetti stokastinen muuttuja, koska se saa
vain erillisiä arvoja. Jälkimmäisessä tapauksessa muuttuja on jatkuva.
Stokastisten muuttujien argumentit on yleensä tapana jättää kirjoittamatta.
Esimerkiksi merkintä X = x tarkoittaa, että stokastinen muuttuja X saa arvon
x.
Noppaesimerkissä merkintä {X = 5} tarkoittaa otosavaruuden osajoukkoa eli
tapahtumaa {(m, n) 
 | X(m, n) = 5}. Vastaavasti tikanheittoesimerkkiin
liittyvä joukko {D < 5} = {(x, y)
| X(m, n) = 5}. Vastaavasti tikanheittoesimerkkiin
liittyvä joukko {D < 5} = {(x, y) 
 | D(x, y) < 5} on tapahtuma.
| D(x, y) < 5} on tapahtuma.
Stokastisten muuttujien saamiin arvoihin liittyvien todennäköisyyksien tarkastelu
johtaa tilastollisten jakaumien tarkasteluun.
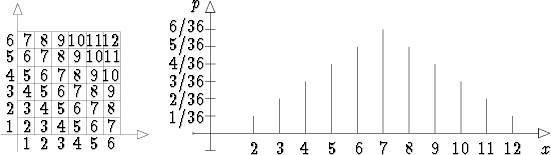
Seuraavissa kuvissa on kahden nopan heittoon liittyvä otosavaruus ja funktion
X(m, n) = m + n sen eri osissa saamat arvot sekä todennäköisyysfunktion
p(x) = P ({X = x}) kuvaaja.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Todennäköisyys
Todennäköisyys  Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
![[#]](kuvat/msam10-c-4.gif) joukko-oppi,
joukko-oppi, ![[#]](kuvat/msam10-c-4.gif) lukumäärän laskeminen,
lukumäärän laskeminen, ![[#]](kuvat/msam10-c-4.gif) funktiokäsite
funktiokäsite
![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka,
tilastomatematiikka, ![[#]](kuvat/msam10-c-4.gif) todennäköisyysjakaumat
todennäköisyysjakaumat
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto
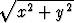 . Muuttujan
. Muuttujan 

