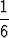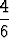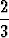Sisällön pääryhmät Todennäköisyys Todennäköisyyslaskenta [ 1 2 3 4 5 6 7 ] ESITIEDOT:  joukko-oppi,  lukumäärän laskeminen,  funktiokäsite KATSO MYÖS:  tilastomatematiikka,  todennäköisyysjakaumat

Kansisivu  Sisältö  Hakemisto

Monissa alkeellisissa todennäköisyyslaskennan probleemoissa otosavaruus on luonnollista valita siten, että alkeistapauksia on äärellinen määrä ja niitä on perusteltua pitää yhtä todennäköisinä. Jos alkeistapausten lukumäärä on n, on jokaisen alkeistapauksen e_k todennäköisyys tällöin P (e_k) = 1/n, k = 1, 2, . . . , n.

Esimerkiksi heitettäessä virheetöntä noppaa tarkoittaa ’virheettömyys’ sitä, että kaikki silmäluvut ovat keskenään yhtä todennäköisiä. Alkeistapauksia on siten kuusi: ’heiton tuloksena on yksi’, ’heiton tuloksena on kaksi’, jne. ja jokaisen todennäköisyys on 1/6, esimerkiksi P ({2}) = 1/6. Erillisten tapahtumien unionia koskeva sääntö antaa tällöin esimerkiksi tapahtuman ’heitto antaa vähintään 3’ todennäköisyydeksi

P ({3, 4, 5, 6}) = P ({3}) + P ({4}) + P ({5}) + P ({6}) = 4 ^.  = = .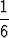

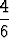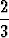Tämäntyyppisissä esimerkeissä todennäköisyys voidaan luonnehtia tapahtuman kannalta suotuisien alkeistapausten ja kaikkien alkeistapausten lukumäärien suhteeksi. Tätä luonnehdintaa kutsutaan klassiseksi todennäköisyydeksi.

Alkeistapausten symmetrisyys ei kuitenkaan välttämättä merkitse sitä, että ne olisivat yhtä todennäköisiä. Jossakin mielessä esimerkiksi poikien ja tyttöjen syntyminen on symmetristä, mutta tilastojen mukaan poikia kuitenkin syntyy hieman enemmän kuin tyttöjä. Tällöin on luontevaa määrittää todennäköisyysfunktio P tilastollisen frekvenssin perusteella, so. määrittämällä riittävän pitkältä ajanjaksolta syntyvien poikien ja tyttöjen prosenttiosuudet. Suomalaisten tilastojen perusteella saadaan tällöin P (poika) 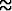0.51 ja P (tyttö) 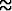0.49.

Tällaisessa tilanteessa puhutaan todennäköisyyden frekvenssitulkinnasta.

Tikanheittoon liittyvien todennäköisyyksien määrittäminen ei ole yhtä helppoa. Ne ilmeisesti riippuvat myös heittäjästä. Määrittäminen voisi tapahtua frekvenssitulkinnan mukaisesti pitkän heittosarjan pohjalta. Tällöin jollakin tavalla tilastoitaisiin tietyn heittäjän saamat tulokset ja näiden avulla luonnehdittaisiin hänen todennäköisyysjakaumansa. Luonnehdinnan tulisi olla sellainen, että sen avulla voidaan ainakin jollakin tarkkuudella määrittää esimerkiksi todennäköisyys, että tikka osuu kahdeksikkoon taulussa ylöspäin osoittavassa 45 asteen sektorissa.

funktio  frekvenssi  tilastotiede (matemaattinen)

Kivelä, niinkuin matematiikka, versio 1.12