Tapahtumien riippumattomuus
Tapahtumat A ja B ovat riippumattomat, jos P (B|A) = P (B), ts. jos tapahtuman
B todennäköisyys ei riipu siitä, onko A sattunut vai ei.
Yhdistämällä tähän ehdollisen todennäköisyyden määritelmä, saadaan
riippumattomille tapahtumille kaava P (A 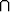 B) = P (A)P (B).
B) = P (A)P (B).
Esimerkkinä olkoon ehdollisen todennäköisyyden laskeminen sille, että toisessa
nopanheitossa saadaan kuutonen sen jälkeen, kun ensimmäisen heiton tuloksena
on ollut kuutonen:
Alkeistapauksia ovat kahdessa heitossa saatavat mahdolliset silmälukuparit. Näitä
on 6 . 6 = 36 kappaletta ja niitä on perusteltua pitää yhtä todennäköisinä jokaisen
todennäköisyyden ollessa 1/36. Jos A tarkoittaa tapahtumaa ’ensimmäinen heitto
antoi kuutosen (ja toinen mitä tahansa)’ ja B tapahtumaa ’toinen heitto antoi
kuutosen (ja ensimmäinen mitä tahansa)’, on
P (A) = 6 . 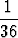 =
= 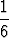 , P (A
, P (A 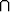 B) =
B) = 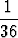 .
.
Ehdollinen todennäköisyys on siis
P (B|A) = 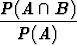 =
= 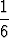 .
.
Tämä on sama kuin P (B), kuten luonnollisesti pitää ollakin, koska perättäiset
nopanheitot eivät millään tavoin riipu toisistaan.
Koska samaa koetta toistettaessa perättäiset toistot ovat toisistaan riippumattomia,
voidaan niiden todennäköisyyksiä laskea helposti: Jos A tarkoittaa tapahtumaa
’ensimmäinen nopanheitto antaa enintään kolmosen’ ja B tapahtumaa ’toinen
heitto antaa vähintään kolmosen’, on todennäköisyys saada ensimmäisellä heitolla
1, 2 tai 3 ja toisella 3, 4, 5 tai 6 kaavan P (A 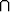 B) = P (A)P (B) mukaisesti
B) = P (A)P (B) mukaisesti
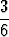 .
. 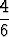 =
= 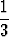 .
.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Todennäköisyys
Todennäköisyys  Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
![[#]](kuvat/msam10-c-4.gif) joukko-oppi,
joukko-oppi, ![[#]](kuvat/msam10-c-4.gif) lukumäärän laskeminen,
lukumäärän laskeminen, ![[#]](kuvat/msam10-c-4.gif) funktiokäsite
funktiokäsite
![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka,
tilastomatematiikka, ![[#]](kuvat/msam10-c-4.gif) todennäköisyysjakaumat
todennäköisyysjakaumat
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto
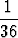
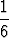
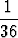
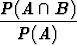
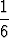
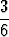
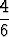
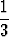 .
.
