![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Todennäköisyys
Todennäköisyys  Tilastomatematiikka [ 1
2 3 4 5 6 7 8 ]
Tilastomatematiikka [ 1
2 3 4 5 6 7 8 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) todennäköisyyslaskenta,
todennäköisyyslaskenta, ![[#]](kuvat/msam10-c-4.gif) todennäköisyysjakaumat,
todennäköisyysjakaumat,
![[#]](kuvat/msam10-c-4.gif) keskiarvo
keskiarvo
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Todennäköisyys Todennäköisyys  Tilastomatematiikka [ 1
2 3 4 5 6 7 8 ] Tilastomatematiikka [ 1
2 3 4 5 6 7 8 ]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) todennäköisyyslaskenta, todennäköisyyslaskenta, ![[#]](kuvat/msam10-c-4.gif) todennäköisyysjakaumat, todennäköisyysjakaumat,
![[#]](kuvat/msam10-c-4.gif) keskiarvo keskiarvo
|
|
Tutkimuksen kohteena olevasta populaatiosta tai siitä muodostetusta otoksesta voidaan koota kahta eri ominaisuutta koskeva data. Tällaisia voivat olla esimerkiksi jonkin koulun oppilaiden päästötodistusten matematiikan ja A-kielen arvosanat. Halutaan selvittää, millainen riippuvuus näiden välillä vallitsee: menestyvätkö matemaattisesti lahjakkaat yleensä hyvin myös kielissä vai keskittyvätkö oppilaat jompaankumpaan toisen jäädessä vähemmälle huomiolle.
Jos tarkastelussa on n oppilasta, joiden matematiikan arvosanat ovat x1, x2, ..., xn ja kieliarvosanat vastaavasti y1, y2, ..., yn, voidaan muodostaa graafinen esitys, jossa pisteet (xk, yk), k = 1, 2, ..., n, sijoitetaan xy-koordinaatistoon. Tämä antaa jo jonkinlaisen kuvan tilanteesta.
Alla olevassa kuvassa on Teknillisen korkeakoulun matematiikan peruskurssin ensimmäisen ja toisen välikokeen tuloksista muodostettu graafinen esitys. Ensimmäisen välikokeen tulokset ovat vaaka-akselilla ja toisen pystyakselilla.
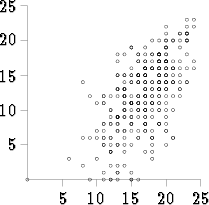
Näyttää ilmeiseltä, että välikoemenestysten välillä on positiivinen riippuvuus, ts. pisteet sijoittuvat nousevan suoran y = kx + b, k > 0, ympärille.
Tarkempi mitta riippuvuudelle on korrelaatiokerroin; ks. seuraavaa.
![[#]](kuvat/msam10-c-4.gif) kulmakerroin kulmakerroin |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12