![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Käyrät ja pinnat
Käyrät ja pinnat  Ympyrä [ 1 2 3 4 5
6 ]
Ympyrä [ 1 2 3 4 5
6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) käyrä,
käyrä, ![[#]](kuvat/msam10-c-4.gif) kulma,
kulma, ![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora
suora
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) toisen asteen käyrät
toisen asteen käyrät
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Käyrät ja pinnat Käyrät ja pinnat  Ympyrä [ 1 2 3 4 5
6 ] Ympyrä [ 1 2 3 4 5
6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) käyrä, käyrä, ![[#]](kuvat/msam10-c-4.gif) kulma, kulma, ![[#]](kuvat/msam10-c-4.gif) piste, piste, ![[#]](kuvat/msam10-c-4.gif) suora suora
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) toisen asteen käyrät toisen asteen käyrät
|
|
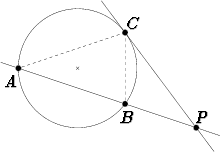
Olkoon P annetun ympyrän ulkopuolinen piste. Asetetaan pisteen P kautta ympyrän sekantti, joka leikkaa ympyrää pisteissä A ja B. Pisteestä P asetettu ympyrän tangentti sivutkoon ympyrää pisteessä C.
Pisteen P potenssiksi ympyrän suhteen sanotaan janojen pituuksien tuloa |P A||P B|, mikä on riippumaton sekantin asemasta ja yhtä suuri kuin tangentilla olevan janan pituuden neliö |P C|2.
Todistus ilmenee seuraavasta kuviosta, missä kolmiot P AC ja P CB ovat yhdenmuotoisia, koska niillä on yhteinen kulma pisteessä P ja toisaalta kulmat P AC ja P CB ovat yhtä suuria samaa kaarta BC vastaavina kehäkulmina. Kolmioiden sivujen verrannollisuudesta seuraa
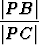 =
= 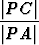 eli |P A||P B| = |P C|2.
eli |P A||P B| = |P C|2.
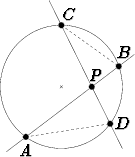
Jos piste P sijaitsee ympyrän sisällä, pätee vastaava. Jos pisteen kautta asetetaan sekantti, joka leikkaa ympyrää pisteissä A ja B, on tulo |P A||P B| riippumaton sekantin asemasta. Tätä kutsutaan ympyrän sisäpuolella olevan pisteen P potenssiksi ympyrän suhteen.
Tulos todistetaan jälleen yhdenmuotoisten kolmioiden avulla. Jos AB ja CD ovat pisteen P kautta kulkevia ympyrän jänteitä, ovat kolmiot AP D ja CP B yhdenmuotoisia ja
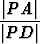 =
= 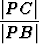 eli |P A||P B| = |P C||P D|.
eli |P A||P B| = |P C||P D|.
Tulo on siis riippumaton siitä, mikä pisteen P kautta kulkeva sekantti on kyseessä.
![[#]](kuvat/msam10-c-4.gif) sekantti (suora) sekantti (suora)![[#]](kuvat/msam10-c-4.gif) tangentti (suora) tangentti (suora)![[#]](kuvat/msam10-c-4.gif) yhdenmuotoisuus (kolmioiden) yhdenmuotoisuus (kolmioiden) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12