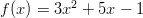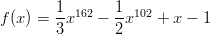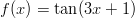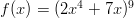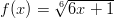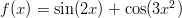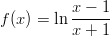Derivaatta

Funktion f derivaattaa pisteessä x merkitään f'(x) (tai Df(x)) ja se voidaan luonnehtia funktion kuvaajalle pisteeseen (x,f(x)) asetetun tangentin kulmakertoimeksi. Monessa mielessä hyödyllisempää on kuitenkin käyttää määritelmänä erotusosamäärän raja-arvoa:
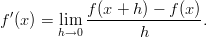
Tämä mahdollistaa mm. differentiaalin käsitteen määrittelyn: differentiaali on tiettyyn pisteeseen liittyvä funktion suoraviivainen (lineaarinen) approksimaatio.
Erotusosamäärän raja-arvoa määritelmänä käyttäen voidaan johtaa melkoinen määrä derivoimiskaavoja, mm. kaikkien ns. alkeisfunktioiden derivaatat. Kaavojen avulla derivoinnista tuleekin sangen mekaaninen operaatio.
 Summan, vakiokerrannaisen, tulon ja osamäärän derivaatta
Summan, vakiokerrannaisen, tulon ja osamäärän derivaatta Yhdistetyn funktion derivaatta
Yhdistetyn funktion derivaatta Käänteisfunktion derivointi
Käänteisfunktion derivointi Luettelo derivaatoista
Luettelo derivaatoista

Esimerkkejä
- Lasketaan derivaatan määritelmää käyttäen
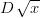 kohdassa
kohdassa
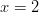 .
.

- Funktioiden
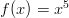 ja
ja 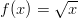 derivaatat.
derivaatat. Esimerkkejä derivaatan laskemisesta erotusosamäärän raja-arvona
Esimerkkejä derivaatan laskemisesta erotusosamäärän raja-arvona
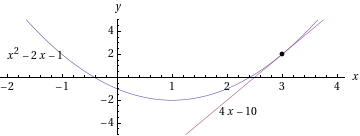
- Lasketaan
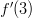 sekä vastaava tangenttisuora, kun
sekä vastaava tangenttisuora, kun 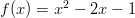 .
.
Funktion tangenttisuora kohdassa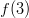 saadaan suoran yhtälöstä
saadaan suoran yhtälöstä
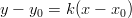 , missä
, missä 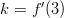 ,
,  sekä
sekä 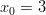 .
.

- Lasketaan
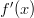 , kun
, kun 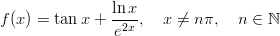 .
.

- Lasketaan
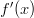 , kun
, kun 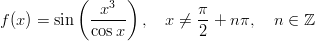 .
.

- (Mma) Derivaatta

Harjoitustehtäviä
- Derivoi:
-
- Derivoi lisää:
-
- Derivoi vielä lisää:
-
- Laske funktioille derivaatta erotusosamäärän raja-arvoa käyttäen:
-
 kohdissa
kohdissa  ja
ja 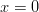
-
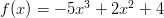 kohdissa
kohdissa 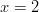 ja
ja 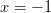
-
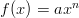
-
- Muodosta funktion
 derivaatta ja tutki, millä
derivaatta ja tutki, millä  :n
arvoilla se on negatiivinen.
:n
arvoilla se on negatiivinen.
- Funktiolla
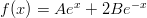 on ominaisuudet
on ominaisuudet 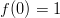 ja
ja
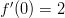 . Määritä kertoimet
. Määritä kertoimet 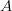 ja
ja 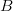 .
.
- Määritä paraabelin
 pisteeseen
pisteeseen 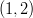 piirretyn
tangentin yhtälö.
piirretyn
tangentin yhtälö.
Tehtävien vastaukset: