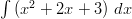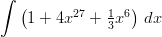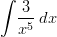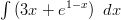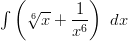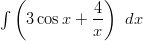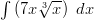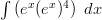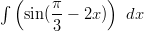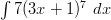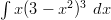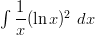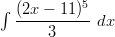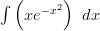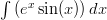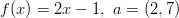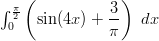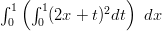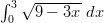Integraali

Määrättyä integraalia

on ajateltava eräänlaisena summan raja-arvona: Lähtökohtana on ns. Riemannin summa

missä luvut x0, x1, …, xn ovat välin [a,b] jakopisteitä ja funktion arvo lasketaan jokaisen osavälin jossakin pisteessä vk. Jos jakopisteiden määrää lisätään, summan termien määrä kasvaa ja samalla jokainen termi lähestyy nollaa osavälien pituuden Δxk mukana. Jos summalla tällöin on raja-arvo — kuten esimerkiksi jatkuvan funktion f tapauksessa on — sanotaan funktiota f integroituvaksi ja raja-arvoa integraaliksi.
Riemannin summa voidaan tulkita käyrän y = f(x) alle jäävän pinta-alan approksimaatioksi, mutta monissa yhteyksissä, varsinkin sovelluksissa, Riemannin summaan ja tätä kautta integraaliin päädytään muunlaisella ajattelulla. Integraali ei siten lainkaan välttämättä kuvaa pinta-alaa, tilavuutta tms. geometrista käsitettä.
 Määrätyn integraalin määrittely
Määrätyn integraalin määrittely Määrätyn integraalin laskusäännöt
Määrätyn integraalin laskusäännöt
Edellisestä täysin erillinen — periaatteessa — näkökulma integraaliin on integraalifunktion käsite. Kyseessä on derivoinnin käänteisoperaatio.
Ehkä jollakin tavoin yllättävää on, että kahdella näkökulmalla on yhteys: määrätty integraali voidaan laskea integraalifunktion avulla.
 Integraalifunktion käsite
Integraalifunktion käsite Määrätyn integraalin ja integraalifunktion yhteys
Määrätyn integraalin ja integraalifunktion yhteys
Määrätyn integraalin laskeminen perustuu siten usein derivoinnin kääntämiseen. Derivoimiskaavoista ja derivointimenettelyistä saadaankin suoraan useita integroimiskaavoja. Integrointi ei kuitenkaan ole samalla tavoin mekaanista kuin derivointi: yksinkertaisillekaan funktioille ei välttämättä löydetä alkeisfunktioiden avulla lausuttavaa integraalifunktiota. Tällöin voidaan turvautua numeeriseen integrointiin, erilaisiin erikoisfunktioihin tms.
 Suoria integrointikaavoja I
Suoria integrointikaavoja I Suoria integrointikaavoja II
Suoria integrointikaavoja II Sijoitusmenettely
Sijoitusmenettely Osittaisintegrointi
Osittaisintegrointi

Esimerkkejä

Koska integroitava lauseke on summa, voidaan se jakaa kahteen erikseen tarkasteltavaan osaan.
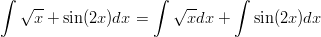
Neliöjuuuri kannattaa muuttaa murtopotenssimuotoon, jolloin sen integroimiseen voidaan käyttää potenssin integroimissääntöä.
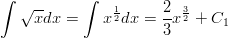
Sinin voimme integroida suoraan ja saadaksemme sisäfunktion
 tarkastellaan derivaattaa
tarkastellaan derivaattaa ![D [− cos(2x )] = 2 sin(2x )](integraali6x.gif) , joka on lähes
sama kuin integroitava funktio. Jos kerromme kummatkin puolet
puolikkaalla, lausekkeet ovat samat.
, joka on lähes
sama kuin integroitava funktio. Jos kerromme kummatkin puolet
puolikkaalla, lausekkeet ovat samat.

Nyt voimme yhdistää saadut integraalit. Merkitsemme
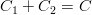 ,
koska integroimisvakio on mielivaltainen.
,
koska integroimisvakio on mielivaltainen.
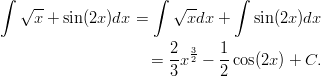
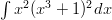
Integroitava lauseke voidaan kertoa auki, mutta siinä syntyy helposti virheitä, kun potenssit kasvavat riittävästi.
Lausekkeessa on nähtävissä sisäfunktion derivoinnin jäljet.
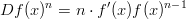
Kaavassa
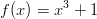 ,
,  ja
ja 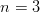 . Derivoidaan
mahdollinen integraalifunktio ja havaitaan derivoinnin tuloksen ja
integroitavan lausekkeen poikkeavan vain vakiokertoimen verran.
. Derivoidaan
mahdollinen integraalifunktio ja havaitaan derivoinnin tuloksen ja
integroitavan lausekkeen poikkeavan vain vakiokertoimen verran.

Integraali on siis.
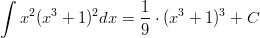
- Riemannin summa käyrän allan olevasta alasta ja määrätyn
integraalin yhteydestä.
 Esimerkki II Riemannin summasta
Esimerkki II Riemannin summasta
- Ilmamäärän määrittäminen Riemannin summalla.
 Esimerkki I Riemannin summasta
Esimerkki I Riemannin summasta
- Määrätty integraali
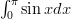 ja käyrien
ja käyrien 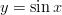 ja
ja 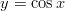 välille
välille ![[0, π] 2](integraali20x.gif) rajaaman alueen pinta-ala.
rajaaman alueen pinta-ala. Esimerkkejä määrätyn integraalin laskemisesta
Esimerkkejä määrätyn integraalin laskemisesta
- Lasketaan käyrien
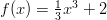 ,
, 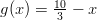 ,
,  ja
x-akselin rajaaman alueen pinta-ala.
ja
x-akselin rajaaman alueen pinta-ala.
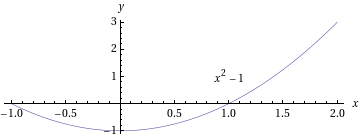
Tarkastellaan ensin missä käyrät leikkaavat ja miltä rajattu alue näyttää.
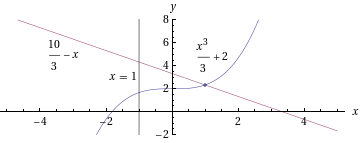
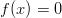 , kun
, kun 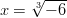 , ja
, ja 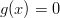 , kun
, kun 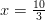 . Kuvaajien
. Kuvaajien
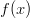 :n ja
:n ja  :n leikkausta tarvitsee tarkastella vain välillä
:n leikkausta tarvitsee tarkastella vain välillä
![√--- [ 3− 6, 103 ]](integraali30x.gif) .
.

Yhtälö toteutuu, kun
 . Jaetaan tarkasteltava pinta-ala kahteen
osaan:
. Jaetaan tarkasteltava pinta-ala kahteen
osaan: ![x ∈ [− 1,1]](integraali33x.gif) ja
ja ![10- x ∈ [1, 3 ]](integraali34x.gif) .
.

Lasketaan kumpikin määrätty integraali erikseen.
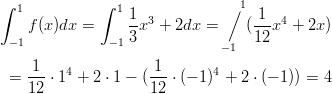
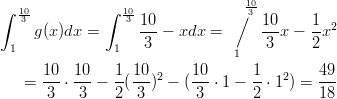
Kysytty pinta-ala on siis

- Määritetään tilavuus, joka syntyy käyrän
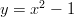 pisteiden
pisteiden
 ja
ja 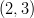 välisen kaaren pyörähtäessa x-akselin ympäri.
välisen kaaren pyörähtäessa x-akselin ympäri.
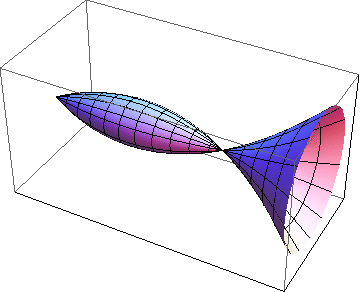
Pyörähdyskappaleen tilavuus saadaan kaavalla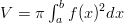 .
.
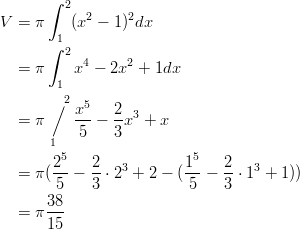
- Sovelletaan osamurtomenetelmää rationaalifunktion integroinnissa.

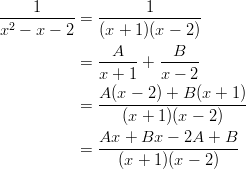
Muodostetaan osoittajista yhtälöpari.
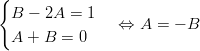
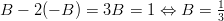
Nyt integraali voidaan jakaa osiin.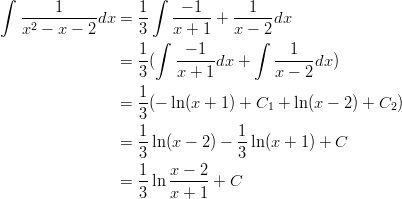
 ja puoliympyrän alan integroiminen.
ja puoliympyrän alan integroiminen.  Esimerkkejä sijoitusmenetelmästä
Esimerkkejä sijoitusmenetelmästä

 Esimerkkejä osittaisintegroinnista
Esimerkkejä osittaisintegroinnista
- Lasketaan funktion
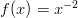 kuvaajan ja x-akselin jäävä pinta-ala,
kun
kuvaajan ja x-akselin jäävä pinta-ala,
kun 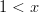 . Pinta-alan integraaliksi saadaan epäoleellinen integraali,
koska ei ole määritelty
. Pinta-alan integraaliksi saadaan epäoleellinen integraali,
koska ei ole määritelty  .
.
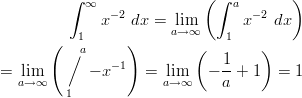
Käyrän alle jäävän alueen pinta-ala on 1.


Harjoitustehtäviä
- Integroi:
-
- Integroi:
-
- Integroi vielä:
-
- Määritä funktiolle
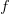 integraalifunktio, joka kulkee pisteen
integraalifunktio, joka kulkee pisteen  kautta.
kautta.
-
- Määrättyjä integraaleja.
-
- Laske seuraavien käyrien ja suorien rajaama pinta-ala:
-
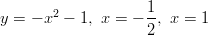 ja x-akseli
ja x-akseli
-
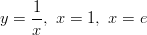 ja
ja 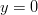
-
 ja x-akseli
ja x-akseli
-
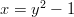 ja
ja 
-
 ja
ja 
-
- Määritä tilavuus, kun
- käyrä
 pyörähtää x-akselin ympäri ja
pyörähtää x-akselin ympäri ja
 .
.
- käyrä
 pyörähtää suoran
pyörähtää suoran  ympäri
ja
ympäri
ja 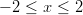 .
.
- käyrä
- Määritä tilavuus, kun käyrien
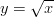 ja
ja  rajaama alue
pyörähtää x-akselin ympäri.
rajaama alue
pyörähtää x-akselin ympäri.
- Laske:

Tehtävien vastaukset: