Sisällön pääryhmät Integraali Määrätty integraali [ 1 2 3 4 5 6 7 8 ] ESITIEDOT:  summa ja tulo,  integraalifunktio KATSO MYÖS:  integroimistekniikkaa

Kansisivu  Sisältö  Hakemisto

Olkoon funktio f jatkuva ja > 0 suljetulla välillä [a, b]. Kuvaajan y = f(x) ja x-akselin väliin jäävän alueen pinta-alaa voidaan approksimoida seuraavalla tavalla:

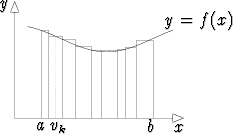
Jaetaan väli [a, b] osaväleihin pisteissä x_k, missä a = x₀ < x₁ < x₂ < ... < x_n = b. Muodostetaan suorakulmiot, joiden kantana on x-akselin osaväli [x_k-1, x_k] (pituudeltaan x_k) ja korkeus määräytyy funktion osavälillä saamien arvojen mukaan: f(v_k), missä v_k [x_k-1, x_k]. Alaa approksimoi tällöin suorakulmioiden pinta-alojen summa

f(v_k)x_k.

Tämä on muodoltaan jälleen Riemannin summa.

Mitä tiheämpi välin [a, b] jako on, sitä tarkemmin suorakulmiot antavat etsityn pinta-alan ja toisaalta sitä lähempänä Riemannin summa on vastaavaa integraalia. Ala on siis sama kuin integraali

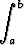f(x) dx.

Edellä sanottu pätee vain, mikäli f(x) > 0 tarkasteluvälillä. Jos f saa negatiivisia arvoja, tulee vastaavan alueen pinta-ala otetuksi huomioon negatiivisena Riemannin summassa ja myös integraalissa.

funktio (reaali-)  jatkuvuus  suljettu väli  kuvaaja  pinta-ala

Kivelä, niinkuin matematiikka, versio 1.12