Sisällön pääryhmät Integraali Määrätty integraali [ 1 2 3 4 5 6 7 8 ] ESITIEDOT:  summa ja tulo,  integraalifunktio KATSO MYÖS:  integroimistekniikkaa

Kansisivu  Sisältö  Hakemisto

Ilmakehän tiheys korkeudella z on karkean mallin mukaan

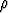(z) = 1.23 e^-0.00012z,

missä korkeus annetaan metreissä ja tiheyden yksikkönä on kg/m³. Sadan kilometrin korkeudessa on ilma jo niin ohutta, että voidaan katsoa ilmakehän kokonaisuudessaan olevan tätä alempana.

Ilmanpaine maanpinnalla aiheutuu yläpuolella olevan ilmamassan painosta. Paine voidaan siis laskea määrittämällä esimerkiksi neliömetrin suuruisen alueen yläpuolella olevan ilmapatsaan massa. Ongelmana on, että ilman tiheys ei ole vakio, vaan pienenee eo. kaavan mukaisesti.

Likimääräisesti ilmamäärä voidaan laskea jakamalla patsas esimerkiksi kilometrin korkuisiin osapatsaisiin ja käyttämällä jokaisen osan tiheydelle osapatsaan puolen välin arvoa. Tällöin saadaan summa

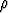(1000k - 500)  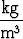 ^. 1 m^2 . 1000 m = 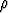(v_k)z_k kg,

missä v_k = 1000k - 500 ja z_k = 1000. Laskemalla summa saadaan 10243.79 kg.

Jos patsas jaetaankin sadan metrin korkuisiin osapatsaisiin, saadaan vastaavalla tavalla

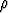(100k - 50)  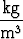 ^. 1 m^2 . 100 m = 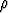(v_k)z_k kg.

Summan arvo on 10249.88 kg.

Kumpikin ovat edellä esitetyn tarkastelun mukaisia Riemannin summia. Jälkimmäinen on saatu edellisestä tihentämällä jakovälien pituudet kymmenesosaan. Jos jakoa edelleen tihennetään, summat lähestyvät ilmakehän paksuuden (0 – 100 000 m) yli otettua integraalia

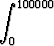
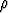(z) dz.

Tämän arvo on 10249.94 kg, kuten integroimalla voidaan todeta. Vertailun vuoksi laskettakoon em. ilmamassan painoisen, neliömetrin alalle sopivan elohopeapatsaan korkeus. Koska elohopean tiheys on 13550 kg/m³, saadaan patsaan korkeudeksi 10250/13550 0.756 metriä, mikä vastaa varsin hyvin normaalia ilmanpainetta 760 mmHg.

eksponenttifunktio  integrointi (kaavat)  integrointi (kaavat)

Kivelä, niinkuin matematiikka, versio 1.12