Sisällön pääryhmät Integraali Määrätty integraali [ 1 2 3 4 5 6 7 8 ] ESITIEDOT:  summa ja tulo,  integraalifunktio KATSO MYÖS:  integroimistekniikkaa

Kansisivu  Sisältö  Hakemisto

Integraalin käsitettä voidaan lähestyä kahdesta näkökulmasta: Integrointi derivoinnin käänteistoimituksena ja integraali tietynlaisena summan raja-arvona. Analyysin peruslause kytkee nämä yhteen.

Historiallisesti jälkimmäinen, integraali summan raja-arvona, on vanhempi. Ensimmäiset merkit tähän suuntaan vievästä ajattelusta on löydettävissä jo vanhalta ajalta Eukleideen Stoikheia-teoksesta ja Arkhimedeen tarkasteluista eräiden pinta-alojen määrittämiseksi. Tällöin puhutaan ekshaustiomenetelmästä; määritettävä pinta-ala ikäänkuin tyhjennetään poistamalla siitä yhä pienempiä suorakulmioita tai muutoin pinta-alaltaan tunnettuja osia.

Pohjois-Italiassa 1600-luvun alkupuolella tarkastelivat Galileo Galilei ja hänen oppilaansa Bonaventura Cavalieri kuvioiden muodostumista jakamattomista osista (’indivisiibeleistä’). Esimerkiksi kolmion voidaan katsoa muodostuvan sen yhden sivun suuntaisista janoista, jotka lyhenevät siirryttäessä kohden vastakkaista kärkeä. Tältä pohjalta määritettiin kuvioiden pinta-aloja. Arabimatemaatikoiden kehittämä algebra oli jo tällöin levinnyt Eurooppaan ja geometristen probleemojen käsittelyssä saatettiin käyttää myös algebrallisia menetelmiä.

1600-luvun loppupuolella aika oli kypsä meidän tuntemamme integraalilaskun syntymiseen. Englantilainen Isaac Newton loi derivoinnin ja sen käänteisoperaationa integroinnin. Samaan aikaan saksalaisen Gottfried Wilhelm Leibniz otti käyttöön määrätyn integraalin käsitteen summan raja-arvona. Molemmat tunsivat integraalilaskun kahden näkökulman välisen yhteyden. Integraalimerkintä 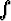f(x) dx on peräisin Leibnizilta. Integraalimerkki on venytetty S, sanan summa alkukirjain.

Määrätyn integraalin täsmällinen määrittely sellaisena kuin se nykyään esitetään on kuitenkin peräisin vasta viime vuosisadalta ranskalaisen Augustin Louis Cauchyn ja saksalaisen Bernhard Riemannin töistä.

Tämän jälkeenkin integraalikäsitettä on yleistetty. Yliopistollisissa peruskursseissa käsitellään yleensä Riemannin integraalia, jolla kuitenkin on rajoituksensa. Pidemmälle menevät matematiikan kurssit edellyttävät ranskalaisen Henri Lebesguen (1875 – 1941) mukaan nimettyä, hieman abstraktimpaa integraalikäsitettä.

Eukleides  Arkhimedes  pinta-ala  Galilei  Cavalieri  algebra  geometria  geometria  Newton  Leibniz  Cauchy  Riemann  Lebesgue

Kivelä, niinkuin matematiikka, versio 1.12