![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Määrätty integraali [ 1 2 3 4
5 6 7 8 ]
Määrätty integraali [ 1 2 3 4
5 6 7 8 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) summa ja tulo,
summa ja tulo, ![[#]](kuvat/msam10-c-4.gif) integraalifunktio
integraalifunktio
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa
integroimistekniikkaa
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Määrätty integraali [ 1 2 3 4
5 6 7 8 ] Määrätty integraali [ 1 2 3 4
5 6 7 8 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) summa ja tulo, summa ja tulo, ![[#]](kuvat/msam10-c-4.gif) integraalifunktio integraalifunktio
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa integroimistekniikkaa
|
|
R-säteisen ympyrän voidaan katsoa muodostuvan samankeskisistä
ympyrärenkaista. Jos ympyrärengas, jonka sisäsäde on rk-1 ja ulkosäde rk,
leikataan poikki ja taivutetaan sisäreunaa sopivasti venyttäen ja ulkoreunaa
sopivasti kuroen suoraksi nauhaksi, saadaan suorakulmio, jonka pinta-ala on
täsmälleen sama kuin ympyrärenkaan pinta-ala. Suorakulmion leveys on tällöin
 rk = rk - rk-1 ja pituus 2
rk = rk - rk-1 ja pituus 2 vk, missä säde vk on valittu sopivasta kohdasta:
rk-1 < vk < rk.
vk, missä säde vk on valittu sopivasta kohdasta:
rk-1 < vk < rk.

Ympyrän ala on tällöin suorakulmioiden alojen summa: 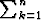 2
2 vk
vk rk. Tämä on
Riemannin summa, joka jakoa tihennettäessä, so. jaettaessa ympyrä yhä useampiin
ja yhä kapeampiin ympyrärenkaisiin, lähenee integraalia
rk. Tämä on
Riemannin summa, joka jakoa tihennettäessä, so. jaettaessa ympyrä yhä useampiin
ja yhä kapeampiin ympyrärenkaisiin, lähenee integraalia
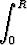 2
2 r dr =
r dr = 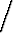
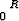
 r2 =
r2 =  R2.
R2.
Ei siis ole sattuma, että ympyrän pinta-alan derivaatta on sen kehän pituus!
![[#]](kuvat/msam10-c-4.gif) ympyrä (esimerkki) ympyrä (esimerkki)![[#]](kuvat/msam10-c-4.gif) ympyrä ympyrä![[#]](kuvat/msam10-c-4.gif) ympyrä (ala) ympyrä (ala) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12