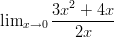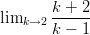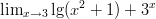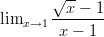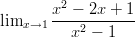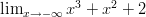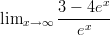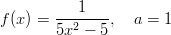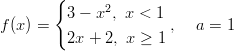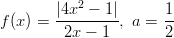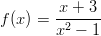Raja-arvo ja jatkuvuus

Raja-arvo on matemaattisen analyysin — differentiaali- ja integraalilaskennan — tärkein peruskäsite. Erikseen puhutaan yleensä lukujonon raja-arvosta ja funktion raja-arvosta.
Havainnollisesti voidaan sanoa, että lukujonon a1, a2, a3, … raja-arvo on a, jos jonon luvut tulevat miten lähelle tahansa lukua a, kun jonossa edetään kyllin pitkälle. Tällaisena määritelmä ei kuitenkaan ole riittävän täsmällinen, jotta sitä voitaisiin soveltaa millaiseen lukujonoon tahansa.
Määritelmä asetetaankin sen takia hieman teknisemmin tarkastelemalla
positiivista etäisyyskynnystä  ja tätä vastaavaa lukujonon indeksiarvoa n0
(joka ilmaisee kuinka mones jonon termi on kyseessä).
ja tätä vastaavaa lukujonon indeksiarvoa n0
(joka ilmaisee kuinka mones jonon termi on kyseessä).
Raja-arvojen laskeminen perustuu määritelmän perusteella todistettaviin lauseisiin. Näiden lisäksi nojaudutaan aiemmin laskettuihin raja-arvoihin, jolloin periaatteessa syntyy puumainen rakenne.
 Lukujonon raja-arvon määritelmä
Lukujonon raja-arvon määritelmä Lukujonon suppeneminen ja hajaantuminen
Lukujonon suppeneminen ja hajaantuminen Lukujonon raja-arvon laskeminen
Lukujonon raja-arvon laskeminen
Funktion f(x) raja-arvo on b muuttujan x lähestyessä arvoa a, jos funktion arvot tulevat miten lähelle tahansa lukua b, kunhan vain x on riittävän lähellä lukua a. Tarkastelun kohteena ovat funktion arvot luvun a ympärillä, mutta funktion arvoa f(a) ei tällöin oteta huomioon; sillä ei ole vaikutusta.
Edellä sanottu ei taaskaan ole riittävän täsmällistä, joten varsinainen määritelmä asetetaan hieman teknisemmin.
Funktioiden raja-arvojen laskeminen tapahtuu hyvin samaan tapaan kuin lukujonojen raja-arvojen laskeminen.
 Funktion raja-arvon määritelmä
Funktion raja-arvon määritelmä Toispuoliset raja-arvot; äärettömyys
Toispuoliset raja-arvot; äärettömyys Funktioiden raja-arvon laskeminen
Funktioiden raja-arvon laskeminen
Reaalimuuttujan reaaliarvoinen funktio on havainnollisesti ottaen jatkuva, jos sen kuvaajassa ei ole hyppykohtia. Matemaattiselle analyysille on tyypillistä, että tämäkään lausuma ei ole riittävän täsmällinen kelvatakseen määritelmäksi.
Raja-arvon käsite tekee kuitenkin määrittelyn helpoksi: funktio on jatkuva tietyllä muuttujan arvolla x = a, jos funktion arvo ja funktion raja-arvo tässä kohdassa ovat yhtä suuret.
Määritelmä pitää sisällään ajatuksen, että raja-arvon tulee olla olemassa. Jos se ei ole olemassa, funktio ei ole jatkuva. Raja-arvon olemassaolo taas voi mitätöityä kahdella tavalla: joko funktion käyttäytyminen kohdan x = a eri puolilla on oleellisesti erilaista (toispuoliset raja-arvot ovat eri suuria) tai funktio käyttäytyy siinä määrin epäsäännöllisesti, että edes toispuoliset raja-arvot eivät ole olemassa.

Esimerkkejä
- Tarkastellaan funktion
 raja-arvoa kun
raja-arvoa kun  lähestyy
seitsemää:
lähestyy
seitsemää:
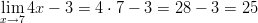
Funktion raja-arvo pisteessä
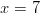 on siis sama kuin funktion arvo
pisteessä
on siis sama kuin funktion arvo
pisteessä 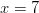 , eli voimme sanoa funktion olevan jatkuva tässä
pisteessä.
, eli voimme sanoa funktion olevan jatkuva tässä
pisteessä.

Päästäksemme juuresta osoittajassa lavennetaan vastaavalla summalla ja sovelletaan binomikaavaa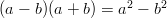 .
.
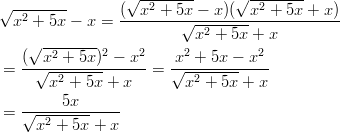
Saatu lauseke voidaan supistaa
 :llä.
:llä.

Lopuksi annamme
 :n kasvaa rajatta.
:n kasvaa rajatta.

Raja-arvon ratkaisu on siis
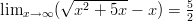 .
.
- Kahden lukujonon raja-arvo äärettömyydessä.
 Esimerkkejä lukujonojen raja-arvoista
Esimerkkejä lukujonojen raja-arvoista
- Tutkitaan funktion
 ,
, 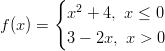 jatkuvuutta
pisteessä
jatkuvuutta
pisteessä 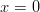 . Aloitetaan tarkastelemalla funktion vasemmanpuoleista
raja-arvoa, eli lähestytään pistettä
. Aloitetaan tarkastelemalla funktion vasemmanpuoleista
raja-arvoa, eli lähestytään pistettä 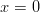 negatiivisesta suunnasta:
negatiivisesta suunnasta:

Oikeanpuoleinen raja-arvo lasketaan vastaavasti:
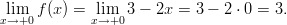
Koska toispuoleiset raja-arvot ovat eri suuret, ei funktio voi olla jatkuva tässä pisteessä. Se on siis funktion epäjatkuvuuspiste.
- Jos funktiolla on kummankinpuoleinen raja-arvo, mutta ne ovat
eri suuret, puhutaan hyppyepäjatkuvuudesta. Funktion kuvaaja
”hyppää”.
 Esimerkkejä funktioiden epäjatkuvuuksista: hyppyepäjatkuvuus
Esimerkkejä funktioiden epäjatkuvuuksista: hyppyepäjatkuvuus
- Jatkuvuuden tarkastelua
 :n ja
:n ja 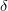 :n avulla.
:n avulla.
(Mma) Jatkuvuus

Harjoitustehtäviä
- Laske raja-arvo:
-
- Laske raja-arvo äärettömyydessä:
-
- Laske toispuoleiset raja-arvot
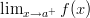 ja
ja 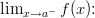
-
- Millä
 :n arvoilla funktio on jatkuva?
:n arvoilla funktio on jatkuva?
- Millä vakion
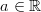 arvolla funktio
arvolla funktio 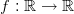 on jatkuva koko
määrittelyjoukossa?
on jatkuva koko
määrittelyjoukossa?
Tehtävien vastaukset: