![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Funktion
jatkuvuus [ 1 2 3 ]
Funktion
jatkuvuus [ 1 2 3 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo
funktion raja-arvo
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) derivaatta
derivaatta
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Funktion
jatkuvuus [ 1 2 3 ] Funktion
jatkuvuus [ 1 2 3 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo funktion raja-arvo
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) derivaatta derivaatta
|
|
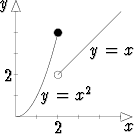
1) Funktiolla on hyppyepäjatkuvuus pisteessä a, jos sekä oikeanpuolinen että vasemmanpuolinen raja-arvo tässä pisteessä on olemassa, mutta ne ovat eri suuret. (Tällöin siis varsinaista raja-arvoa ei ole.) Epäjatkuvuuden kannalta on epäolennaista, mikä funktion arvo f(a) on; se voi yhtyä jompaankumpaan toispuolisista raja-arvoista tai olla jotakin muuta.
Esimerkiksi funktiolla
f(x) = 
on hyppyepäjatkuvuus pisteessä x = 2.
2) Määrittelemällä
f(x) = 
saadaan funktio, jolla on raja-arvo 4 pisteessä x = 2, mutta tämä poikkeaa funktion arvosta f(2) = 0. Funktio on siis tässä pisteessä epäjatkuva.
3) Esimerkki yhdellä lausekkeella määritellystä funktiosta, jolla on
hyppyepäjatkuvuus, on f(x) = arctan(1/x). Tarkkaan ottaen tämä ei
ole määritelty origossa, mutta on luontevaa määritellä sen arvoksi
jompikumpi toispuolisista raja-arvoista - /2 tai
/2 tai  /2, jolloin origoon syntyy
hyppyepäjatkuvuus.
/2, jolloin origoon syntyy
hyppyepäjatkuvuus.
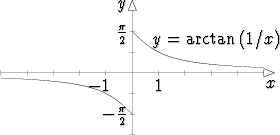
![[#]](kuvat/msam10-c-4.gif) raja-arvo (funktion) raja-arvo (funktion)![[#]](kuvat/msam10-c-4.gif) raja-arvo (toispuolinen) raja-arvo (toispuolinen) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12