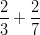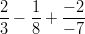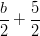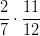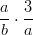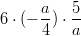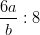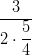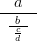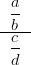Luvut

Luvut ja toisaalta geometriset käsitteet muodostavat matematiikan lähtökohdan. Reaaliluvuilla tai niitä esittävillä symboleilla — kirjaimilla — laskeminen onkin perustaito: laskutoimitusten vaihdannaisuus, osittelulait, murtolukujen laskusäännöt, lausekkeiden sieventäminen ja muokkaaminen muilla tavoilla.
 Luonnolliset, kokonais-, rationaaliluvut
Luonnolliset, kokonais-, rationaaliluvut Irrationaaliluvut
Irrationaaliluvut Desimaaliesitys
Desimaaliesitys Laskulait
Laskulait Murtoluvuilla laskeminen
Murtoluvuilla laskeminen
Symbolisten murtolukulausekkeiden käsittely voi joskus olla hankalaa ja edellyttää laskusääntöjen — algebran — hyvää hallintaa.
Itseisarvo käsitteenä on varsin yksinkertainen, mutta itseisarvolausekkeiden käsittelyssä on omat taitonsa.
Lukualuetta voidaan laajentaa reaaliluvuista edelleen kompleksiluvuiksi, mutta nämä eivät kuulu tämän esityksen piiriin.

Esimerkkejä
- Luvun 378 alkutekijähajotelma on:
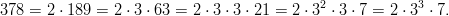
- Lukujen 24 ja 36 suurin yhteinen tekijä (syt) ja pienin yhteinen jaettava
(pyj) saadaan seuraavanlaisesti:
Aluksi jaetaan kumpikin luku alkutekijöihinsä.
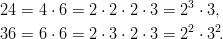
Tämän jälkeen on helppo käydä läpi kummankin alkutekijähajotelmat ja muodostaa yhdistävistä tekijöistä tulo, joka on lukujen suurin yhteinen tekijä:
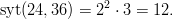
Koska alkutekijähajotelmat ovat yksikäsitteisiä, saadaan pyj poimimalla jokainen esiintyvä alkuluku, nostamalla se korkeampaan hajotelmissa esiintyvistä potensseista ja muodostamalla näistä tulo:
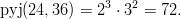
- Aina ei kannata käyttää murtolukujen yhteenlaskukaavaa, koska
summan laskemiseksi riittää saada nimittäjät samoiksi. Esimerkiksi
summassa
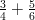 nimittäjien pienin yhteinen jaettava on pienempi kuin
niiden tulo:
nimittäjien pienin yhteinen jaettava on pienempi kuin
niiden tulo:
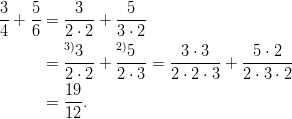
- Itseisarvomerkkien poistaminen:
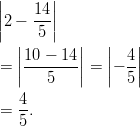
- Itseisarvomerkkien poistaminen:
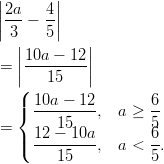

Harjoitustehtäviä
- Laske:
-
- Laske:
-
- Laske:
-
- Laske:
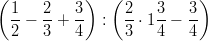
- Laske:

- Polttomoottorin mäntä suorittaa yhden kierroksen aikana edestakaisen liikkeen ylhäältä alas ja takaisin. Auton moottorin kierroslukumittarin osoittaessa 4000 kierrosta minuutissa auton pyörä pyörähtää 780 kierrosta minuutissa. Pyörän halkaisija on 73 cm. Moottorin männän ylhäältä alas kulkema matka eli iskun pituus on 70 mm. Kun autolla ajetaan 60 km, kuinka pitkän matkan mäntä kaiken kaikkiaan kulkee liikkuessaan edestakaisin?
Tehtävien vastaukset: