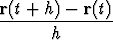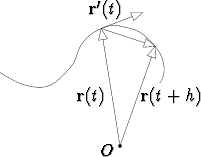Käyrän tangentti
Parametriesityksen avulla annetun taso- tai avaruuskäyrän tangentin suuntavektori,
tangenttivektori, saadaan yksinkertaisesti derivoimalla parametriesitys:
r'(t) = x'(t) i + y'(t) j tai r'(t) = x'(t) i + y'(t) j + z'(t) k.
Tulos seuraa siitä, että r(t + h) - r(t) on kahta käyrän pistettä yhdistävä
vektori, so. vektori, joka antaa käyrän erään sekantin suunnan. Tämän kanssa
samansuuntainen on vektori
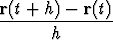 .
.
Jos h  0, lähestyvät pisteet toisiaan, jolloin sekantti kääntyy tangentiksi, ja
toisaalta yo. erotusosamäärävektori lähestyy derivaattaa r'(t).
0, lähestyvät pisteet toisiaan, jolloin sekantti kääntyy tangentiksi, ja
toisaalta yo. erotusosamäärävektori lähestyy derivaattaa r'(t).
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Käyrät ja pinnat
Käyrät ja pinnat  Käyrä [ 1 2 3 4
]
Käyrä [ 1 2 3 4
]
![[#]](kuvat/msam10-c-4.gif) funktiokäsite,
funktiokäsite, ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) yhtälöt,
yhtälöt, ![[#]](kuvat/msam10-c-4.gif) koordinaatistot,
koordinaatistot,
![[#]](kuvat/msam10-c-4.gif) piste
piste
![[#]](kuvat/msam10-c-4.gif) suora,
suora, ![[#]](kuvat/msam10-c-4.gif) derivaatta,
derivaatta, ![[#]](kuvat/msam10-c-4.gif) tangentti ja normaali,
tangentti ja normaali, ![[#]](kuvat/msam10-c-4.gif) pinta
pinta
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto