Sisällön pääryhmät Geometrian peruskäsitteet Taso [ 1 2 3 4 5 ] ESITIEDOT:  vektori,  koordinaatistot,  piste,  suora KATSO MYÖS:  geometria,  vektorialgebra,  geometriset probleemat

Kansisivu  Sisältö  Hakemisto

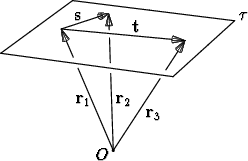
Tasolle voidaan muodostaa vektoriesitys samaan tapaan kuin suoralle:

Olkoon annettuna kolme avaruuden pistettä paikkavektoreidensa avulla: P₁  r₁, P₂  r₂, P₃  r₃. Oletetaan, että nämä eivät ole samalla suoralla, jolloin ne määräävät yksikäsitteisesti tason .

Erotusvektorit s = r₂ - r₁ ja t = r₃ - r₁ ovat tason suuntaisia. Ne ovat keskenään eri suuntaisia, koska pisteet P₁, P₂, P₃ eivät ole samalla suoralla. Jos vektorit asetetaan alkamaan pisteestä P₁, ne määräävät suorat, jotka puolestaan määräävät tason . Tämän johdosta vektoreita kutsutaan tason virittäjävektoreiksi.

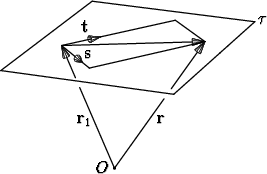
Jos P   r on mikä tahansa tason piste, sen paikkavektori voidaan kirjoittaa muotoon r = r₁ + a s + b t, kun skalaarit a ja b valitaan sopivasti. Toisaalta jos a ja b ovat mitä tahansa reaalilukuja, antaa eo. lauseke aina jonkin tasossa olevan pisteen paikkavektorin.

Esitystä r = r₁ + a s + b t, missä a, b , kutsutaan tason vektoriesitykseksi. Tässä on kaksi parametria, a ja b, joiden arvoja vaihtelemalla saadaan kaikki tason pisteet. Samoin kuin suoran tapauksessa tason vektoriesitys ei ole yksikäsitteinen. Tason vektoriesitys muodostaa vektorialgebrallisen työkalun geometristen ongelmien käsittelyyn.

vektori  paikkavektori  skalaari  geometria (vektori-)

Kivelä, niinkuin matematiikka, versio 1.12