![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometrian peruskäsitteet
Geometrian peruskäsitteet  Taso [ 1 2 3
4 5 ]
Taso [ 1 2 3
4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) vektori,
vektori, ![[#]](kuvat/msam10-c-4.gif) koordinaatistot,
koordinaatistot, ![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora
suora
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) geometria,
geometria, ![[#]](kuvat/msam10-c-4.gif) vektorialgebra,
vektorialgebra, ![[#]](kuvat/msam10-c-4.gif) geometriset probleemat
geometriset probleemat
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Geometrian peruskäsitteet Geometrian peruskäsitteet  Taso [ 1 2 3
4 5 ] Taso [ 1 2 3
4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) vektori, vektori, ![[#]](kuvat/msam10-c-4.gif) koordinaatistot, koordinaatistot, ![[#]](kuvat/msam10-c-4.gif) piste, piste, ![[#]](kuvat/msam10-c-4.gif) suora suora
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) geometria, geometria, ![[#]](kuvat/msam10-c-4.gif) vektorialgebra, vektorialgebra, ![[#]](kuvat/msam10-c-4.gif) geometriset probleemat geometriset probleemat
|
|
xy-tasossa muotoa ax + by + c = 0 oleva yhtälö esittää suoraa. Tämän analogia kolmiulotteisessa xyz-avaruudessa on yhtälö ax + by + cz + d = 0; se esittää tasoa. Perustelut ovat hyvin samankaltaiset kuin suoran tapauksessa:
Olkoon annettuna piste P0  r0, jonka kautta taso
r0, jonka kautta taso  kulkee ja tasoa vastaan
kohtisuora vektori, sen normaalivektori n. Nämä määräävät tason yksikäsitteisesti.
kulkee ja tasoa vastaan
kohtisuora vektori, sen normaalivektori n. Nämä määräävät tason yksikäsitteisesti.
Jotta piste P  r olisi tasossa, on vektoreiden n ja r - r0 oltava toisiaan vastaan
kohtisuorat: n . (r - r0) = 0.
r olisi tasossa, on vektoreiden n ja r - r0 oltava toisiaan vastaan
kohtisuorat: n . (r - r0) = 0.
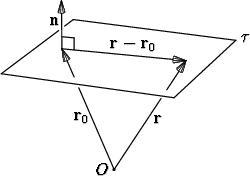
Kun merkitään r = x i + y j + z k, r0 = x0 i + y0 j + z0 k, n = a i + b j + c k, saa ehto muodon
n . (r - r0) = a(x - x0) + b(y - y0) + c(z - z0) = 0
eli
ax + by + cz + d = 0,
missä on merkitty d = -ax0 - by0 - cz0. Tämä on tason yhtälö xyz-koordinaatistossa.
Koordinaattien x, y ja z kertoimina ovat normaalivektorin komponentit.
Piste (x, y, z) on siis tasossa  , jos ja vain jos ehto ax + by + cz + d = 0
toteutuu.
, jos ja vain jos ehto ax + by + cz + d = 0
toteutuu.
![[#]](kuvat/msam10-c-4.gif) koordinaatisto (xy-) koordinaatisto (xy-)![[#]](kuvat/msam10-c-4.gif) koordinaatisto (xyz-) koordinaatisto (xyz-)![[#]](kuvat/msam10-c-4.gif) vektori vektori![[#]](kuvat/msam10-c-4.gif) skalaaritulo skalaaritulo![[#]](kuvat/msam10-c-4.gif) komponentti komponentti |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12