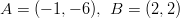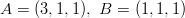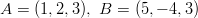Piste, suora, taso

Piste ja suora, kolmiulotteisessa avaruudessa myös taso ovat geometrisia peruskäsitteitä. Niitä voidaan tarkastella ’sellaisinaan’, synteettisen geometrian keinoin Eukleideen tapaan. Tällöin suoran määrää yksikäsitteisesti kaksi pistettä ja tason kolme pistettä, jotka eivät saa olla samalla suoralla.
Vaihtoehtoisesti voidaan käyttää vektoreita, jolloin päädytään vektorigeometriaan, tai koordinaattiesityksiä, jolloin päädytään koordinaattigeometriaan.
Vektorigeometriassa piste esitetään paikkavektorilla, so. origosta pisteeseen osoittavalla vektorilla. Jos käytetään koordinaatteja, pisteen paikka määräytyy tasossa kahdella ja avaruudessa kolmella koordinaatilla. Nämä ovat usein suorakulmaisia xy- tai xyz-koordinaatteja, mutta myös napa- tai pallokoordinaatteja voidaan käyttää.
 Pisteen identifiointi
Pisteen identifiointi Pisteen paikkavektori erilaisissa koordinaatistoissa
Pisteen paikkavektori erilaisissa koordinaatistoissa Kahden pisteen etäisyys
Kahden pisteen etäisyys
Ehkä helpoin tapa suorien laskennalliseen käsittelyyn on vektoriesityksen käyttäminen. Tästä voidaan tarvittaessa purkaa perinteinen analyyttisessa geometriassa käytetty suoran yhtälö. Joissakin tapauksissa kulmakertoimen käyttäminen on näppärää, mutta vektoriesityksen suuntavektori kattaa paremmin kaikki tilanteet: y-akselin suuntaisella suoralla ei ole kulmakerrointa; avaruussuoraa ei edes voida esittää yhdellä yhtälöllä.
 Suoran vektoriesitys
Suoran vektoriesitys Suoran yhtälö
Suoran yhtälö Suoran kulmakerroin
Suoran kulmakerroin Kulmakertoimen laskeminen
Kulmakertoimen laskeminen
Kaksiulotteisen tason suoraa vastaa kolmiulotteisessa avaruudessa taso. Tasolla on vektoriesitys samaan tapaan kuin tasogeometrian suoralla ja tästä voidaan purkaa analyyttisessa geometriassa perinteisesti käytetty tason yhtälö. Avaruussuoraa ei voida esittää yhdellä yhtälöllä, vaan sitä on ajateltava kahden tason leikkaussuorana, jolloin yhtälöitä on kaksi.
 Tason vektoriesitys
Tason vektoriesitys Tason yhtälö
Tason yhtälö Suora kolmiulotteisessa avaruudessa
Suora kolmiulotteisessa avaruudessa

Esimerkkejä
- Suorien
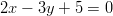 ja
ja 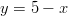 yhteiset pisteet saadaan
muodostamalla yhtälöpari.
yhteiset pisteet saadaan
muodostamalla yhtälöpari.
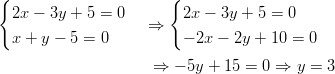
Ratkaistaan
 sijoittamalla
sijoittamalla 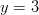 jälkimmäiseen suoraan.
jälkimmäiseen suoraan.

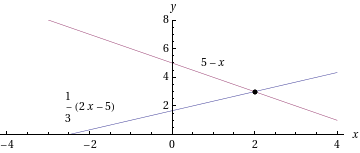
Suorat leikkaavat pisteessä
 .
. 
- Muunnetaan ratkaistuun muotoon suora
 .
.
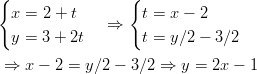
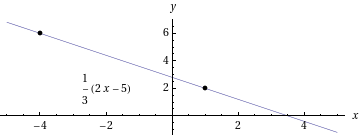
Suoran ratkaistu muoto on
 .
.
- Määritetään pisteiden
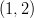 ja
ja  kautta kulkevan suoran
yhtälö.
kautta kulkevan suoran
yhtälö.
Määritetään suoran kulmakerroin .
.
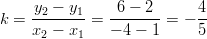
Suoran kulmakerroin on negatiivinen eli suora on laskeva. Sijoitetaan ensimmäinen piste ja saatu kulmakerroin suoran yhtälöön
 .
.

Pisteiden kautta kulkevan suoran yhtälö on
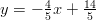 .
. 
- Selvitetään ovatko pisteet
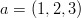 ,
, 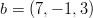 ja
ja
 samalla suoralla.
samalla suoralla.
Muodostetaan vektorit pisteiden ja
ja  sekä
sekä  ja
ja  välille. Jos
pisteet ovat samalla suoralla, nämä vektorit ovat yhdensuuntaisia.
välille. Jos
pisteet ovat samalla suoralla, nämä vektorit ovat yhdensuuntaisia.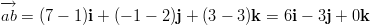
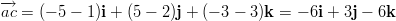
Vektorit ovat yhdensuuntaiset, jos on olemassa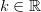 , siten että
, siten että

Tälläistä vakiota
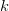 ei ole olemassa, eli pisteet eivät ole samalla
suoralla.
ei ole olemassa, eli pisteet eivät ole samalla
suoralla.
- Tutkitaan ovatko tasot
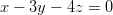 ja
ja 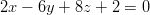 yhdensuuntaiset.
yhdensuuntaiset.
Riittää tutkia ovatko tasojen normaalit yhdensuuntaiset, eli onko olemassa kerrointa siten että
siten että 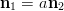 . Tasojen eräät
normaalit saadaan tasojen yhtälöiden kertoimista:
. Tasojen eräät
normaalit saadaan tasojen yhtälöiden kertoimista: 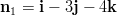 ja
ja
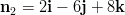 .
.
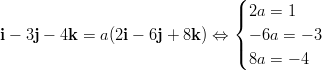
Kun ratkaistaan kaksi ensimmäistä yhtälöä, saadaan
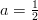 , mutta
kolmannesta tulee
, mutta
kolmannesta tulee 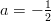 . Ei siis ole olemassa kerrointa, jolla normaalit
olisivat samat, eli tasot eivät ole yhdensuuntaiset.
. Ei siis ole olemassa kerrointa, jolla normaalit
olisivat samat, eli tasot eivät ole yhdensuuntaiset. 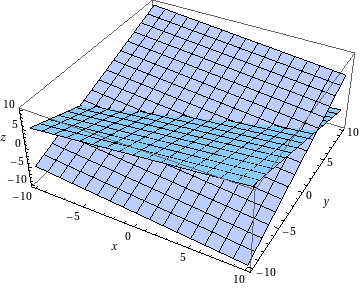
- Olkoon suora
 .
.
Suoran suuntavektori on
on  , ja suoran normaalivektori
, ja suoran normaalivektori  saadaan yhtälöstä
saadaan yhtälöstä 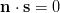 .
.

Esimerkiksi
 ja
ja  toteuttavat yhtälön, eli vektori
toteuttavat yhtälön, eli vektori
 on eräs suoran normaalivektoreista. Normaalivektorin ja
suoran pisteen
on eräs suoran normaalivektoreista. Normaalivektorin ja
suoran pisteen 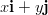 avulla saamme yhtälön xy-tason muotoon:
avulla saamme yhtälön xy-tason muotoon:

Huomataan, että suoran yhtälön kertoimet vastaavat sen normaalivektorin kertoimia.

Harjoitustehtäviä
- Määritä suoran yhtälö, kun suora kulkee pisteiden
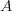 ja
ja 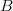 kautta.
kautta.
-
- Määritä suoran parametriesitys, kun suora kulkee pisteiden
 ja
ja 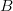 kautta.
kautta.
-
- Ovatko suorat yhdensuuntaiset?
-
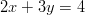 ja
ja 
-
 ja
ja 
-
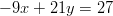 ja
ja 
-
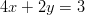 ja
ja 
-
- Ovatko pisteet samalla suoralla?
-
- Millä
 :n arvoilla suorat
:n arvoilla suorat  ja
ja  ovat
yhdensuuntaiset? Kohtisuorat?
ovat
yhdensuuntaiset? Kohtisuorat?
- Mikä suora
- on suoran
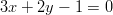 suuntainen ja kulkee pisteen
suuntainen ja kulkee pisteen
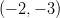 kautta?
kautta?
- on kohtisuorassa suoraa
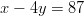 ja kulkee pisteen
ja kulkee pisteen  kautta?
kautta?
- on suoran
- Ovatko pisteet
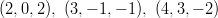 ja
ja 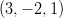 samassa
tasossa?
samassa
tasossa?