![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ]
Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) määrätty integraali
määrätty integraali
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa,
integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) pinta-aloja ja tilavuuksia
pinta-aloja ja tilavuuksia
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ] Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa, integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) pinta-aloja ja tilavuuksia pinta-aloja ja tilavuuksia
|
|
Olkoon tarkasteltavana kappale, jonka läpi x-akseli kulkee. Jaetaan tämä
ohuisiin viipaleisiin x-akselia vastaan kohtisuorilla tasoilla. Olkoon kappaleen
tasoleikkauksen pinta-ala A(vj), kun leikkaava taso on kohdassa x = vj. Jos
tässä kohdassa olevan viipaleen paksuus on  xj, on viipaleen tilavuus
A(vj)
xj, on viipaleen tilavuus
A(vj) xj. Koko kappaleen tilavuutta approksimoi Riemannin summa
xj. Koko kappaleen tilavuutta approksimoi Riemannin summa
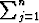 A(vj)
A(vj) xj, missä summeeraus ulotetaan kaikkiin viipaleisiin. Viipaleita
ohennettaessa tämä johtaa kappaleen tilavuutta esittävään määrättyyn
integraaliin
xj, missä summeeraus ulotetaan kaikkiin viipaleisiin. Viipaleita
ohennettaessa tämä johtaa kappaleen tilavuutta esittävään määrättyyn
integraaliin
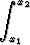 A(x) dx,
A(x) dx,
missä x1 ja x2 ovat kappaleen äärimmäisten pisteiden x-koordinaatit.
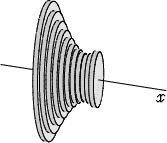
Yleensä x-akseli mielletään vaakasuoraksi. Edellä olevassa tarkastelussa akselin ei välttämättä tarvitse olla vaakasuora, vaan aivan yhtä hyvin kelpaa minkä suuntainen akseli tahansa, kunhan akselia vastaan kohtisuorien tasoleikkausten pinta-ala on laskettavissa.
![[#]](kuvat/msam10-c-4.gif) Riemannin summa Riemannin summa![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12