Sisällön pääryhmät Integraali Pinta-alojen ja tilavuuksien laskeminen [ 1 2 3 4 5 6 ] ESITIEDOT:  määrätty integraali KATSO MYÖS:  integroimistekniikkaa,  pinta-aloja ja tilavuuksia

Kansisivu  Sisältö  Hakemisto

Pallonmuotoisen öljysäiliön säde on R ja säiliössä on öljyä korkeuteen h saakka; 0 < h < 2R. Mikä on öljyn tilavuus?

Sijoitetaan kolmiulotteinen xyz-koordinaatisto siten, että origo on pallonmuotoisen säiliön keskipisteessä. Symmetria-akseliksi valitaan pystysuora z-akseli.

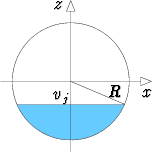
Korkeudella z = v_j oleva vaakasuora tasoleikkaus on tällöin ympyrä, jonka säde on Pythagoraan mukaan 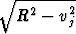. Tasoleikkauksen ala on siten A(v_j) = (R² - v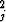). Vaakasuoran öljyviipaleen tilavuutta esittää tällöin lauseke A(v_j)z_j ja koko öljymäärää Riemannin summa 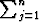A(v_j)z_j, missä summeerataan kaikki öljykerrokset huomioon ottaen.

Öljymäärä sijaitsee säiliössä alueella, missä z-koordinaatit ovat välillä [-R, h - R]. (Jos h = 0, saadaan vain säiliön alin piste z = -R; jos h = 2R, on öljyä välillä [-R, R], so. koko pallossa.) Riemannin summaa vastaa tällöin integraali

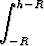
(R² - z²) dz,

mikä antaa öljytilavuudeksi

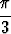h²(3R - h).

Jos erityisesti h = 2R, saadaan pallon tilavuus R³.

pallo  koordinaatisto (xyz-)  ympyrä  Pythagoraan lause  Riemannin summa  väli (reaaliakselin)  määrätty integraali  integrointi (kaavat)  integrointi (kaavat)  integrointi (sijoitus)  integrointi (osittais-)  pallo (tilavuus)

Kivelä, niinkuin matematiikka, versio 1.12