![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ]
Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) määrätty integraali
määrätty integraali
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa,
integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) pinta-aloja ja tilavuuksia
pinta-aloja ja tilavuuksia
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ] Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa, integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) pinta-aloja ja tilavuuksia pinta-aloja ja tilavuuksia
|
|
Jos funktio f saa välillä [a, b] vain ei-negatiivisia arvoja, so. f(x) > 0, kun
x  [a, b], voidaan kuvaajan y = f(x), x-akselin ja suorien x = a, x = b rajaaman
alueen pinta-ala laskea suoraan integraalista
[a, b], voidaan kuvaajan y = f(x), x-akselin ja suorien x = a, x = b rajaaman
alueen pinta-ala laskea suoraan integraalista 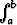 f(x) dx.
f(x) dx.
Jos välillä [a, b] on f(x) < 0, antaa integraali vastaavan pinta-alan negatiivisena.
Jos funktio vaihtaa merkkiään välillä [a, b], ottaa integraali x-akselin ylä- ja alapuolella olevien alueiden alat huomioon positiivisina ja negatiivisina kuvan osoittamalla tavalla. Jos kaikkien osa-alueiden alat halutaan positiivisina, on väli [a, b] jaettava osiin funktion f nollakohdissa, laskettava erikseen integraali jokaisen osavälin yli ja tuloksia yhteenlaskettaessa otettava osaintegraalien merkit huomioon.
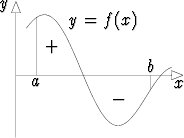
Usein on yksinkertaisinta ajatella, että laskettava ala jaetaan kapeisiin pystysuoriin suorakulmioihin ja summeerataan näiden pinta-alat positiivisina. Tällöin saadaan Riemannin summa, joka jakoa tihennettäessä, so. suorakulmioita kavennettaessa johtaa määrättyyn integraaliin. Tämä ajattelu toimii myös, kun laskettavana on kahden käyrän väliin jäävä ala.
![[#]](kuvat/msam10-c-4.gif) funktio (reaali-) funktio (reaali-)![[#]](kuvat/msam10-c-4.gif) väli (reaaliakselin) väli (reaaliakselin)![[#]](kuvat/msam10-c-4.gif) kuvaaja kuvaaja![[#]](kuvat/msam10-c-4.gif) pinta-ala pinta-ala![[#]](kuvat/msam10-c-4.gif) määrätty
integraali määrätty
integraali![[#]](kuvat/msam10-c-4.gif) Riemannin summa Riemannin summa![[#]](kuvat/msam10-c-4.gif) käyrä (taso-) käyrä (taso-) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12