![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ]
Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) määrätty integraali
määrätty integraali
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa,
integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) pinta-aloja ja tilavuuksia
pinta-aloja ja tilavuuksia
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ] Pinta-alojen ja tilavuuksien
laskeminen [ 1 2 3 4 5 6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa, integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) pinta-aloja ja tilavuuksia pinta-aloja ja tilavuuksia
|
|
Pyörähtäköön käyrä y = f(x), x1 < x < x2, x-akselin ympäri, jolloin
syntyy pyörähdyspinta. Tämän pinta-ala voidaan laskea jakamalla pinta
ympyränmuotoisiin suikaleisiin x-akselia vastaan kohtisuorilla tasoilla. Jokainen
suikale on likimain katkaistu kartio. Tämän ala on  (r1 + r2)s, missä r1 ja r2 ovat
ala- ja yläpohjan säteet sekä s sivujanan pituus.
(r1 + r2)s, missä r1 ja r2 ovat
ala- ja yläpohjan säteet sekä s sivujanan pituus.
Jos leikkaustasot sijaitsevat kohdissa x = xj, ovat pohjien säteet f(xj-1) ja f(xj). Sivujanan pituus on Pythagoraan mukaan
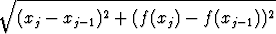 | ||||
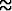 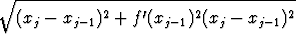 = = 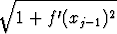  xj, xj, |
 xj = xj - xj-1.
Summeeraamalla suikaleiden pinta-alat saadaan
xj = xj - xj-1.
Summeeraamalla suikaleiden pinta-alat saadaan
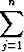
 (f(xj-1) + f(xj))
(f(xj-1) + f(xj))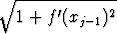
 xj.
xj.
Tämä ei ole Riemannin summa (koska funktioiden arvoja on laskettu sekä pisteessä xj-1 että pisteessä xj), mutta voidaan kuitenkin osoittaa, että jakoa tihennettäessä päädytään integraaliin
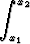 2
2 f(x)
f(x)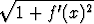 dx,
dx,
joka siis esittää pyörähdyspinnan alaa.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12