![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Todennäköisyys
Todennäköisyys  Todennäköisyysjakaumat [
1 2 3 4 5 ]
Todennäköisyysjakaumat [
1 2 3 4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) todennäköisyyslaskenta,
todennäköisyyslaskenta, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali
määrätty integraali
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka
tilastomatematiikka
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Todennäköisyys Todennäköisyys  Todennäköisyysjakaumat [
1 2 3 4 5 ] Todennäköisyysjakaumat [
1 2 3 4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) todennäköisyyslaskenta, todennäköisyyslaskenta, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka tilastomatematiikka
|
|
Jatkuva stokastinen muuttuja X saa reaaliarvoja joltakin reaaliakselin väliltä [a, b] (tai mahdollisesti kaikki reaaliarvot). Tällöin yksittäisen reaaliarvon todennäköisyys on = 0, vaikka arvo ei olekaan mahdoton. Sen sijaan todennäköisyys, että arvo osuu jollekin osavälille [c, d], on yleensä positiivinen.
Jatkuvan muuttujan X jakauma, ns. jatkuva jakauma määritellään yleensä tiheysfunktion f(x) avulla. Tämä on kaikkialla > 0 ja todennäköisyys, että muuttujan X arvo on välillä [c, d], saadaan integraalista:
P (c < X < d) = 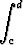 f(x) dx.
f(x) dx.
Jos integroidaan satunnaismuuttujan kaikkien mahdollisten arvojen muodostaman
välin yli (voidaan ajatella koko reaaliakselin yli), on kyseessä varma tapahtuma ja
siis 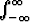 f(x) dx = 1.
f(x) dx = 1.
Yksinkertainen esimerkki jatkuvasta jakaumasta on tasainen jakauma välillä [a, b]. Tämän tiheysfunktio on
f(x) = ![1
{ -----, kun x (- [a,b],
b- a
0 muulloin.](kuvat/isom1394x.gif)
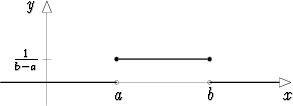
Jatkuvia jakaumia on paljon muitakin; erityisen tärkeä on normaalijakauma, jota käsitellään edempänä.
![[#]](kuvat/msam10-c-4.gif) stokastinen muuttuja (jatkuva) stokastinen muuttuja (jatkuva)![[#]](kuvat/msam10-c-4.gif) väli (reaaliakselin) väli (reaaliakselin)![[#]](kuvat/msam10-c-4.gif) todennäköisyys
(funktio) todennäköisyys
(funktio)![[#]](kuvat/msam10-c-4.gif) todennäköisyys (funktio) todennäköisyys (funktio)![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali![[#]](kuvat/msam10-c-4.gif) tapahtuma
(todennäköisyyslaskennassa) tapahtuma
(todennäköisyyslaskennassa) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12