![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Todennäköisyys
Todennäköisyys  Todennäköisyysjakaumat [
1 2 3 4 5 ]
Todennäköisyysjakaumat [
1 2 3 4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) todennäköisyyslaskenta,
todennäköisyyslaskenta, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali
määrätty integraali
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka
tilastomatematiikka
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Todennäköisyys Todennäköisyys  Todennäköisyysjakaumat [
1 2 3 4 5 ] Todennäköisyysjakaumat [
1 2 3 4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) todennäköisyyslaskenta, todennäköisyyslaskenta, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka tilastomatematiikka
|
|
Erilaisia jakaumia pyritään luonnehtimaan sopivilla tunnusluvuilla.
Tärkein näistä on odotusarvo, jota voidaan luonnehtia stokastisen muuttujan saamien arvojen painotetuksi keskiarvoksi, jossa painoina ovat todennäköisyydet.
Jos diskreetti satunnaismuuttuja X saa arvot xk todennäköisyyksillä pk, odotusarvo on
E(X) = 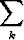 xkpk.
xkpk.
Jos jatkuvan satunnaismuuttujan tiheysfunktio on f(x), on odotusarvo
E(X) = 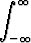 xf(x) dx.
xf(x) dx.
Tämäkin on todennäköisyyksillä painotettu keskiarvo, kuten nähdään tarkastelemalla integraalia vastaavaa Riemannin summaa. Esimerkiksi yhden nopan heitossa odotusarvo on
1 . 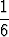 + 2 .
+ 2 . 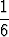 + 3 .
+ 3 . 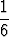 + 4 .
+ 4 . 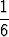 + 5 .
+ 5 . 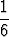 + 6 .
+ 6 . 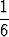 = 3.5 ;
= 3.5 ;
kyseessä on silmälukujen suora keskiarvo, koska kaikki pistetodennäköisyydet ovat samoja.
Binomijakauman ja väliä [a, b] vastaavan tasaisen jakauman odotusarvoiksi saadaan
 k
k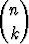 pk(1 - p)n-k = np ja
pk(1 - p)n-k = np ja 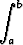
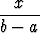 dx =
dx = 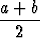 .
.
Jakauman laajuutta — hajontaa — odotusarvon E(X) = 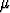 ympärillä voidaan
mitata tarkastelemalla etäisyyttä |X -
ympärillä voidaan
mitata tarkastelemalla etäisyyttä |X - 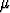 | (joka itse on stokastinen muuttuja).
Tämän neliön odotusarvo on jakauman varianssi:
| (joka itse on stokastinen muuttuja).
Tämän neliön odotusarvo on jakauman varianssi:
 2 = E((X -
2 = E((X - 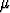 )2).
)2).
Varianssin neliöjuuri  =
= 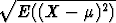 on jakauman keskihajonta.
Diskreetin ja jatkuvan jakauman tapauksessa varianssille voidaan johtaa
lausekkeet
on jakauman keskihajonta.
Diskreetin ja jatkuvan jakauman tapauksessa varianssille voidaan johtaa
lausekkeet
 2 =
2 = 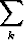 (xk -
(xk - 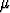 )2pk ja
)2pk ja  2 =
2 = 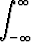 (x -
(x - 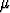 )2f(x) dx.
)2f(x) dx.
Näiden avulla saadaan esimerkiksi binomijakauman varianssiksi np(1 - p) ja tasaisen jakauman varianssiksi (b - a)2/12.
![[#]](kuvat/msam10-c-4.gif) stokastinen muuttuja (diskreetti) stokastinen muuttuja (diskreetti)![[#]](kuvat/msam10-c-4.gif) stokastinen muuttuja (jatkuva) stokastinen muuttuja (jatkuva)![[#]](kuvat/msam10-c-4.gif) keskiarvo
(painotettu) keskiarvo
(painotettu)![[#]](kuvat/msam10-c-4.gif) summamerkintä summamerkintä![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali![[#]](kuvat/msam10-c-4.gif) Riemannin summa Riemannin summa![[#]](kuvat/msam10-c-4.gif) keskihajonta keskihajonta![[#]](kuvat/msam10-c-4.gif) keskihajonta keskihajonta |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12