Sisällön pääryhmät Todennäköisyys Todennäköisyysjakaumat [ 1 2 3 4 5 ] ESITIEDOT:  todennäköisyyslaskenta,  määrätty integraali KATSO MYÖS:  tilastomatematiikka

Kansisivu  Sisältö  Hakemisto

Diskreetin tai jatkuvan stokastisen muuttujan X kertymäfunktioksi kutsutaan funktiota F (x) = P (X < x). Koska kyseessä on todennäköisyys, on 0 < F (x) < 1 kaikilla x. Funktio on kaikkialla kasvava (so. jos x₁ < x₂, niin F (x₁) < F (x₂); funktio voi siis olla paloittain vakio).

Diskreetin satunnaismuuttujan kertymäfunktio on porrasfunktio; esimerkkinä olkoon kahta noppaa heitettäessä saatavan pistesumman kertymäfunktio:

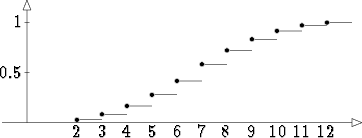
Jatkuvan jakauman kertymäfunktiolle F (x) ja tiheysfunktiolle f(x) pätee

F (x) = P (X < x) = 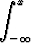f(x) dx.

Jos tiheysfunktio on jatkuva, pätee myös

F '(x) = f(x).

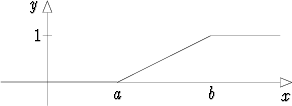
Esimerkkinä jatkuvan satunnaismuuttujan kertymäfunktiosta olkoon väliä [a, b] vastaavan tasaisen jakauman kertymäfunktio:

F (x) =

stokastinen muuttuja (diskreetti)  stokastinen muuttuja (jatkuva)  todennäköisyys (funktio)  todennäköisyys (funktio)  kasvava (funktio)  kasvava (funktio)  määrätty integraali  jatkuvuus  derivoituvuus  integraalifunktio

Kivelä, niinkuin matematiikka, versio 1.12