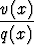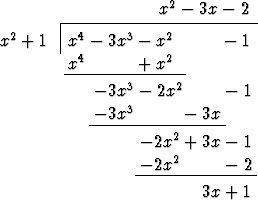Polynomien jakolasku
Polynomien jakolasku voidaan tehdä jakokulmassa. Yleensä ei ole mielekästä jakaa
alempiasteista polynomia korkeampiasteisella. Lähtökohtana on siis seuraava:
Olkoon annettuna yhden muuttujan polynomit p(x) ja q(x), missä p(x) on
vähintään samaa astetta kuin q(x). On etsittävä osamääräpolynomi u(x) ja
jakojäännöspolynomi v(x) siten, että
 = u(x) +
= u(x) + 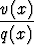 ,
,
ts. ’jakolaskun tulos on osamäärä plus jakojäännös jaettuna jakajalla’. Sama
voidaan kirjoittaa myös muotoon
p(x) = q(x)u(x) + v(x),
ts. ’jaettava on jakaja kertaa osamäärä plus jakojäännös’.
Jakolaskua yleensä jatketaan niin pitkälle, että jakojäännös on alhaisempaa
astetta kuin jakaja.
Olkoon esimerkiksi p(x) = x4 - 3x3 - x2 - 1 ja q(x) = x2 + 1. Jakolasku näyttää
tällöin seuraavalta:
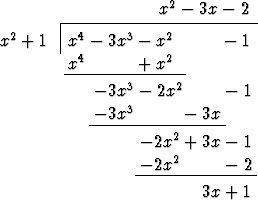
Osamäärä on siis u(x) = x2 - 3x - 2 ja jakojäännös v(x) = 3x + 1.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Potenssit ja polynomit
Potenssit ja polynomit  Polynomit [ 1 2 3
4 ]
Polynomit [ 1 2 3
4 ]
![[#]](kuvat/msam10-c-4.gif) summa ja tulo
summa ja tulo
![[#]](kuvat/msam10-c-4.gif) potenssi,
potenssi, ![[#]](kuvat/msam10-c-4.gif) polynomien tekijöihin jako,
polynomien tekijöihin jako, ![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt,
polynomiyhtälöt,
![[#]](kuvat/msam10-c-4.gif) binomi- ja multinomikertoimet,
binomi- ja multinomikertoimet, ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot
reaalifunktiot
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto