Polynomifunktio
Reaalialueen polynomifunktion
p(x) = anxn + an-1xn-1 + ... + a1x + a0
kuvaajalla on eräitä sille luonteenomaisia piirteitä.
Jos polynomi on ensimmäistä astetta, sen kuvaaja on suora. Toisen asteen
polynomin kuvaaja on paraabeli, joka aukeaa ylöspäin, jos toisen asteen termin
kerroin on positiivinen, ja alaspäin, jos se on negatiivinen. Kolmannen asteen
polynomin kuvaajaa kutsutaan usein kuutioparaabeliksi.
Yleisesti polynomifunktion kuvaajalla on seuraavat ominaisuudet:
Jos polynomi on parillista astetta ja korkeimman asteen termin kerroin an on
positiivinen, käyrä katoaa äärettömyyteen positiivisen y-akselin suunnassa,
kun argumentti x etääntyy origosta riittävän pitkälle; raja-arvojen avulla
ilmaistuna: limx ±
± p(x) = +
p(x) = + . Jos an on negatiivinen, on vastaavasti
limx
. Jos an on negatiivinen, on vastaavasti
limx ±
± p(x) = -
p(x) = - .
.
Jos polynomi on paritonta astetta ja an > 0, argumentin x kasvaessa kuvaaja
tulee negatiivisen y-akselin suunnasta ja jollakin tavoin heilahdeltuaan katoaa
positiivisen y-akselin suuntaan: limx -
- p(x) = -
p(x) = - , limx
, limx +
+ p(x) = +
p(x) = + . Jos
an < 0, raja-arvot kääntyvät toisinpäin. Kummassakin tapauksessa funktio saa
kaikki reaaliarvot.
. Jos
an < 0, raja-arvot kääntyvät toisinpäin. Kummassakin tapauksessa funktio saa
kaikki reaaliarvot.
Funktion kuvaaja mutkittelee äärettömyyteen menojen välissä — jonkinlaisella
keskialueella — siten, että suora voi leikata sitä enintään asteluvun osoittamassa
määrässä pisteitä.
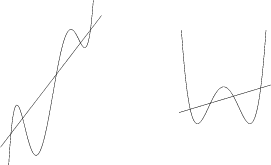
Viidennen ja neljännen asteen polynomien kuvaajat:
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Potenssit ja polynomit
Potenssit ja polynomit  Polynomit [ 1 2 3
4 ]
Polynomit [ 1 2 3
4 ]
![[#]](kuvat/msam10-c-4.gif) summa ja tulo
summa ja tulo
![[#]](kuvat/msam10-c-4.gif) potenssi,
potenssi, ![[#]](kuvat/msam10-c-4.gif) polynomien tekijöihin jako,
polynomien tekijöihin jako, ![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt,
polynomiyhtälöt,
![[#]](kuvat/msam10-c-4.gif) binomi- ja multinomikertoimet,
binomi- ja multinomikertoimet, ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot
reaalifunktiot
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto ±
±


