![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometriset probleemat
Geometriset probleemat  Synteettistä
geometriaa [ 1 2 ]
Synteettistä
geometriaa [ 1 2 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora,
suora, ![[#]](kuvat/msam10-c-4.gif) taso
taso
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) kolmio,
kolmio, ![[#]](kuvat/msam10-c-4.gif) kulma,
kulma, ![[#]](kuvat/msam10-c-4.gif) ympyrä
ympyrä
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Geometriset probleemat Geometriset probleemat  Synteettistä
geometriaa [ 1 2 ] Synteettistä
geometriaa [ 1 2 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) piste, piste, ![[#]](kuvat/msam10-c-4.gif) suora, suora, ![[#]](kuvat/msam10-c-4.gif) taso taso
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) geometriset probleemat, geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) kolmio, kolmio, ![[#]](kuvat/msam10-c-4.gif) kulma, kulma, ![[#]](kuvat/msam10-c-4.gif) ympyrä ympyrä
|
|
Olkoon tehtävänä todistaa, että kolmion keskijanat leikkaavat toisensa samassa pisteessä, joka jakaa kunkin keskijanan suhteessa 2 : 1 kärjestä vastaisen sivun keskipisteeseen lukien.
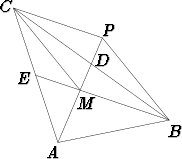
Kolmion ABC kaksi keskijanaa olkoot AD ja BE ja näiden leikkauspiste M. Tavoitteena on osoittaa, että |BM| : |ME| = 2 : 1. Tätä varten tehdään seuraava apupiirros: Jatketaan keskijanaa AD osan MD pituisella janalla DP . Yhdistetään piste P pisteisiin B ja C sekä piste C pisteeseen M.
Keskijanan määritelmän mukaan ovat janat BD ja DC yhtä pitkät; apukonstruktiosta seuraa, että myös MD ja DP ovat yhtä pitkät. Kolmiot MDC ja P DB ovat tällöin yhtenevät (SKS), mistä seuraa, että janat BP ja MC ovat yhtä pitkät ja yhdensuuntaiset. Nelikulmio BP CM on siis suunnikas. Suunnikkaan vastakkaisina sivuina ovat janat BM ja P C yhtä pitkät.
Kolmiot AP C ja AME ovat yhdenmuotoiset (KK), koska suorat BM ja P C ovat
suunnikkaan sivuina yhdensuuntaiset. Yhdenmuotoisuussuhde on 2, koska jana
AC on kaksi kertaa janan AE pituinen. Tällöin pätee janojen pituuksille myös
|ME| =  |P C| =
|P C| =  |BM|, jolloin |BM| : |ME| = 2.
|BM|, jolloin |BM| : |ME| = 2.
Vastaavasti voidaan osoittaa, että piste M jakaa janan AD suhteessa 2 : 1.
Toistamalla päättely siten, että keskijanan AD sijasta käytetään kärjestä C lähtevää keskijanaa CF , todetaan, että kaikki keskijanat leikkaavat toisensa samassa pisteessä M, joka jakaa keskijanat suhteessa 2 : 1.
Esitetty todistus lepää kolmioiden yhtenevyyttä ja yhdenmuotoisuutta koskevien tulosten varassa. Tämä on tyypillistä matemaattisille todistuksille yleensäkin: Tulosten — lauseiden tai teoreemojen — todistamisessa nojaudutaan aiemmin todistettuihin lauseisiin. Jostakin on kuitenkin lähdettävä liikkeelle. Pohjana ovat tällöin ns. aksioomat, lausumat, joita sovitaan pidettävän tosina. Elementaarigeometriassa niiden voidaan sanoa olevan tosia ’itsestäänselvyytensä’ takia; yleisemmin voidaan sanoa, että ne ovat tosia, koska tarkastelun kohde tulee määritellyksi sen kautta, että esitetyt aksioomat ovat voimassa!
![[#]](kuvat/msam10-c-4.gif) kolmio kolmio![[#]](kuvat/msam10-c-4.gif) keskijana (esimerkki) keskijana (esimerkki)![[#]](kuvat/msam10-c-4.gif) keskijana (esimerkki) keskijana (esimerkki)![[#]](kuvat/msam10-c-4.gif) keskijana (esimerkki) keskijana (esimerkki)![[#]](kuvat/msam10-c-4.gif) keskijana keskijana![[#]](kuvat/msam10-c-4.gif) yhtenevyys (kolmioiden) yhtenevyys (kolmioiden)![[#]](kuvat/msam10-c-4.gif) suunnikas suunnikas![[#]](kuvat/msam10-c-4.gif) yhdenmuotoisuus
(kolmioiden) yhdenmuotoisuus
(kolmioiden)![[#]](kuvat/msam10-c-4.gif) yhdenmuotoisuussuhde yhdenmuotoisuussuhde![[#]](kuvat/msam10-c-4.gif) aksiooma aksiooma![[#]](kuvat/msam10-c-4.gif) aksiooma aksiooma |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12