Sisällön pääryhmät Geometriset probleemat Synteettistä geometriaa [ 1 2 ] ESITIEDOT:  piste,  suora,  taso KATSO MYÖS:  geometriset probleemat,  kolmio,  kulma,  ympyrä

Kansisivu  Sisältö  Hakemisto

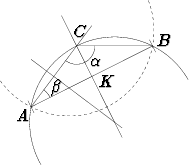
Olkoon tehtävänä konstruoida ne tason pisteet, joista katsottaessa annettu jana näkyy annetun suuruisessa kulmassa. Välineiksi sallitaan viivoitin ja harppi klassisen geometrian tapaan.

Olkoon siis annettuna jana AB ja kulma (< 180^o). Tehtävä voidaan ratkaista seuraavasti:

Piirretään janalle AB keskinormaali, so. suora, joka on kohtisuorassa janaa vastaan ja kulkee sen keskipisteen K kautta. Tämä voidaan tehdä harpilla ja viivoittimella.

Piirretään kulma, jonka kärkenä on piste A, toisena kylkenä jana AB ja jonka suuruus on 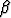= 90^o - /2; tämäkin voidaan tehdä harpilla ja viivoittimella. Kulman toisen kyljen ja keskinormaalin leikkauspiste olkoon C.

Piirretään ympyrä, joka kulkee pisteiden A, C ja B kautta. Tämä voidaan tehdä etsimällä janojen AB ja AC keskinormaalit, joiden leikkauspiste on ympyrän keskipiste.

Etsityt pisteet sijaitsevat ympyränkaarella ACB tai tämän kanssa symmetrisellä janan AB toisella puolella sijaitsevalla ympyrän kaarella.

Ratkaisu vaatii perustelut: Miksi on saatu juuri ne pisteet, joita etsittiin?

Kulman ACB suuruus on 2(90^o - 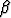) = . Piste C on siis ainakin yksi etsityistä pisteistä. Samaa jännettä vastaavat ympyrän kehäkulmat ovat yhtä suuria (= puolet vastaisen kaaren asteluvusta); jana AB näkyy siis samansuuruisessa kulmassa jokaisesta kaaren ABC pisteestä.

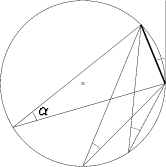
Vastaava tilanne kulman ollessa pienempi (symmetrinen ympyränkaari puuttuu):

jana  kulma (taso-)  keskinormaali (janan)  ympyrä  kaari  jänne  kehäkulma (esimerkki)  kehäkulma (esimerkki)  kehäkulma

Kivelä, niinkuin matematiikka, versio 1.12