Esimerkki 2 vektorigeometriasta
Olkoon todistettavana, että puoliympyrän sisältämä kehäkulma on suora.
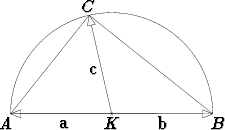
Puoliympyrän säde olkoon r. Keskipisteestä K halkaisijan AB päätepisteisiin
osoittavat vektorit olkoot a ja b; kummankin pituus on = r ja b = -a. Sijaitkoon
piste C jossakin puoliympyrän kehällä. Keskipisteestä tähän osoittava vektori
olkoon c, jonka pituus myös on = r.
Kulma ACB on tällöin puoliympyrän sisältämä kehäkulma. Sen kylkivektoreiden
skalaaritulo on
(a - c) . (b - c) = (a - c) . (-a - c) = -a . a + c . c = -r2 + r2 = 0.
Koska skalaaritulo on = 0, on vektoreiden välinen kulma suora.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometriset probleemat
Geometriset probleemat  Vektorigeometriaa
[ 1 2 3 ]
Vektorigeometriaa
[ 1 2 3 ]
![[#]](kuvat/msam10-c-4.gif) vektori,
vektori, ![[#]](kuvat/msam10-c-4.gif) vektorialgebra,
vektorialgebra, ![[#]](kuvat/msam10-c-4.gif) koordinaatistot,
koordinaatistot, ![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora,
suora,
![[#]](kuvat/msam10-c-4.gif) taso
taso
![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) kolmio,
kolmio, ![[#]](kuvat/msam10-c-4.gif) kulma,
kulma, ![[#]](kuvat/msam10-c-4.gif) ympyrä
ympyrä
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto
