Esimerkki 2 algebrallisista menetelmistä geometriassa
Janan kultaisella leikkauksella tarkoitetaan sen jakamista kahteen osaan siten, että
koko janan pituuden suhde isompaan osaan on sama kuin isomman osan suhde
pienempään osaan. Jos janan pituus on a ja isomman osan pituus x, tulee siis
olla
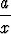 =
= 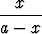 .
.
Tämä johtaa toisen asteen yhtälöön x2 + ax - a2 = 0, jolla on ratkaisuna
x = -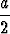 ±
± 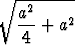 .
.
Miinusmerkki juuren edessä ei tule kysymykseen, koska jananpituuden x tulee
olla positiivinen. Tulokseksi saadaan sievennysten jälkeen
x = 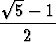 a.
a.
Pituudeltaan a olevan janan kultainen leikkaus on saadun lausekkeen perusteella
myös konstruoitavissa geometrisesti, so. harpilla ja viivoittimella. Tätä varten
piirretään ensin suorakulmainen kolmio, jonka kateetit ovat a ja a/2;
hypotenuusa on tällöin Pythagoraan lauseen mukaan 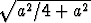 . Kun tästä
erotetaan (harpilla) pois toinen kateetti a/2, jää jäljelle etsitty jana x.
Piirrä!
. Kun tästä
erotetaan (harpilla) pois toinen kateetti a/2, jää jäljelle etsitty jana x.
Piirrä!
Janan kultainen leikkaus (lat. sectio aurea), jota usein kutsutaan myös janan
jakamiseksi jatkuvaan suhteeseen, oli jo Pythagoraan aikana tunnettu. Varsinkin
keskiajalla kultainen leikkaus oli suuren huomion kohteena ja sitä pidettiin
taiteessa perustavan tärkeänä. Esimerkiksi rakennuksen ikkuna-aukkojen
sopusuhtaisuuden on katsottu vaativan sivujen pituuksien mitoittamista kultaisen
leikkauksen suhteeseen.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometriset probleemat
Geometriset probleemat  Algebralliset
menetelmät geometriassa [ 1 2 3 ]
Algebralliset
menetelmät geometriassa [ 1 2 3 ]
![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt,
polynomiyhtälöt, ![[#]](kuvat/msam10-c-4.gif) Pythagoraan lause,
Pythagoraan lause, ![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora,
suora,
![[#]](kuvat/msam10-c-4.gif) taso
taso
![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) kolmio,
kolmio, ![[#]](kuvat/msam10-c-4.gif) ympyrä,
ympyrä, ![[#]](kuvat/msam10-c-4.gif) pallo,
pallo,
![[#]](kuvat/msam10-c-4.gif) monikulmiot,
monikulmiot, ![[#]](kuvat/msam10-c-4.gif) monitahokkaat
monitahokkaat
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto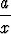
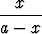
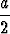
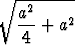
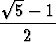
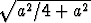 . Kun tästä
erotetaan (harpilla) pois toinen kateetti
. Kun tästä
erotetaan (harpilla) pois toinen kateetti 