Esimerkki 3 algebrallisista menetelmistä geometriassa
Pallon sisään sijoitetaan säännöllinen tetraedri siten, että sen kärjet ovat pallon
pinnalla. On määritettävä pallon säteen ja tetraedrin särmän suhde. Olkoon
pallon säde r ja tetraedrin särmän pituus a.

Säännöllisen tetraedrin sivutahkot ovat tasasivuisia kolmioita. Tetraedrin
korkeusjana kohtaa vastaisen sivutahkon sen keskipisteessä, joka on myös
keskijanojen leikkauspiste ja siis jakaa keskijanat suhteessa 2 : 1.
Oheiset kuviot esittävät tetraedria pohjatahkon vastaisine korkeuksineen sekä
pallon ja tetraedrin leikkausta sellaisella tasolla, joka kulkee pallon keskipisteen ja
tetraedrin kahden kärjen kautta.
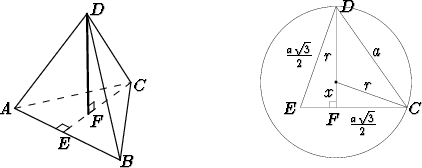
Kuvioiden perusteella saadaan Pythagoraan lausetta käyttäen yhtälöt
r2 = x2 + 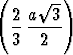 2, a2 = (r + x)2 +
2, a2 = (r + x)2 + 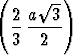 2.
2.
Näistä on eliminoitava x, jolloin saadaan pituuksien a ja r välinen ehto.
Helpoimmin eliminointi tapahtuu ratkaisemalla edellisestä yhtälöstä a2 ja
sijoittamalla se jälkimmäiseen. Tällöin saadaan 2(r2 - x2) = (r + x)2, mikä
voidaan jakaa tekijällä r + x (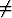 0). Tuloksena on x = r/3 ja tämän perusteella
a/r = 2
0). Tuloksena on x = r/3 ja tämän perusteella
a/r = 2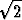 /
/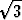 .
.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometriset probleemat
Geometriset probleemat  Algebralliset
menetelmät geometriassa [ 1 2 3 ]
Algebralliset
menetelmät geometriassa [ 1 2 3 ]
![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt,
polynomiyhtälöt, ![[#]](kuvat/msam10-c-4.gif) Pythagoraan lause,
Pythagoraan lause, ![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora,
suora,
![[#]](kuvat/msam10-c-4.gif) taso
taso
![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) kolmio,
kolmio, ![[#]](kuvat/msam10-c-4.gif) ympyrä,
ympyrä, ![[#]](kuvat/msam10-c-4.gif) pallo,
pallo,
![[#]](kuvat/msam10-c-4.gif) monikulmiot,
monikulmiot, ![[#]](kuvat/msam10-c-4.gif) monitahokkaat
monitahokkaat
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto

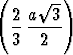
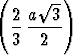
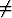
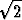
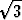 .
. 