Esimerkki 1 algebrallisista menetelmistä geometriassa
Olkoon annettuna janat, joiden pituudet ovat a ja b. Tehtävänä on geometrisesti
konstruoida — harpilla ja viivoittimella — jana, jonka pituus on näiden
keskiverto, so. 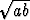 .
.
Asetetaan annetut janat toistensa jatkeeksi. Yhdistetty jana olkoon AB; janoja
erottava piste tämän keskellä olkoon C. Piirretään puoliympyrä, jonka
halkaisijana on AB, ja pisteeseen C janan AB normaali. Tämä leikatkoon
puoliympyrän pisteessä D. Jnan CD pituus olkoon x.
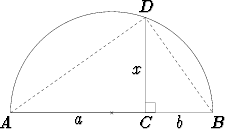
Pituus x voidaan laskea seuraavalla tavalla.
Puoliympyrän sisältämänä kehäkulmana kulma ADB on suora kulma. Koska
kulmien CAD ja CDB vasemmat kyljet ovat toisiaan vastaan kohtisuorassa,
samoin oikeat, niin kulmat ovat yhtä suuret. Kolmioissa ACD ja DCB ovat
lisäksi kulmat ACD ja DCB suorina kulmina yhtä suuria, ja siis kolmiot
ovat yhdenmuotoiset (KK). Niiden vastinsivut ovat tällöin verrannollisia,
jolloin
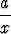 =
= 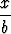 ,
,
mistä seuraa x = 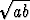 . Jana CD on pituudeltaan siis annettujen janojen
keskiverto.
. Jana CD on pituudeltaan siis annettujen janojen
keskiverto.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometriset probleemat
Geometriset probleemat  Algebralliset
menetelmät geometriassa [ 1 2 3 ]
Algebralliset
menetelmät geometriassa [ 1 2 3 ]
![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt,
polynomiyhtälöt, ![[#]](kuvat/msam10-c-4.gif) Pythagoraan lause,
Pythagoraan lause, ![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora,
suora,
![[#]](kuvat/msam10-c-4.gif) taso
taso
![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) kolmio,
kolmio, ![[#]](kuvat/msam10-c-4.gif) ympyrä,
ympyrä, ![[#]](kuvat/msam10-c-4.gif) pallo,
pallo,
![[#]](kuvat/msam10-c-4.gif) monikulmiot,
monikulmiot, ![[#]](kuvat/msam10-c-4.gif) monitahokkaat
monitahokkaat
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto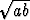 .
.

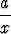
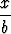
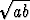 . Jana
. Jana 