Sisällön pääryhmät Kulma, kolmio, monikulmio ja -tahokas Monikulmiot [ 1 2 3 4 5 ] ESITIEDOT:  kolmio KATSO MYÖS:  geometriset probleemat

Kansisivu  Sisältö  Hakemisto

Säännöllisten monikulmioiden sivujen pituuksia voidaan usein laskea algebrallisen geometrian keinoin. Toisaalta myös kompleksilukuaritmetiikkaa voidaan hyödyntää.

Jos säännöllinen n-kulmio sijoitetaan siten, että sen keskipiste on origossa ja kärjet R-säteisellä origokeskisellä ympyrällä, saadaan kärkien koordinaatit kompleksilukuina helposti muodossa Ru^k, missä u = cos(2/n) + i sin(2/n) on kompleksinen kiertotekijä. Indeksin k eri arvot antavat eri kärjet; k = 0, 1, 2, ..., n - 1. Menettely on luonteeltaan numeerinen, koska sinin ja kosinin tarkkojen arvojen laskeminen ei yleensä ole helppoa.

Esimerkkinä algebrallisten menetelmien käytöstä olkoon säännöllisen kymmenkulmion sivun pituuden x määrittäminen, kun kulmio on piirretty R-säteisen ympyrän sisään.

Yhdistämällä ympyrän keskipiste kahteen peräkkäiseen kymmenkulmion kärkeen saadaan tasakylkinen kolmio, jonka kulmat ovat 36^o, 72^o ja 72^o. Puolittamalla toinen kantakulma saadaan seuraava kuvio:

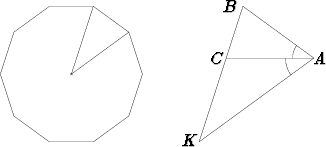
Kolmiot KAB ja ABC ovat yhdenmuotoiset, koska kummassakin on kulmat 36^o ja 72^o. Kolmiot ACK ja BAC ovat tasakylkisiä ja siis |AB| = |AC| = |CK| = x. Yhdenmuotoisten kolmioiden vastinsivut ovat verrannollisia, jolloin

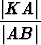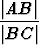= eli = .

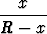Tästä seuraa

x = ( 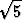- 1)R.

(Vrt. kultaiseen leikkaukseen.)

kompleksiluku  sini  kosini  kiertotekijä  tasakylkinen  kulma (taso-)  yhdenmuotoisuus (kolmioiden)  kultainen leikkaus

Kivelä, niinkuin matematiikka, versio 1.12