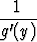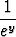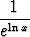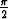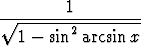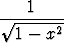![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Derivaatta
Derivaatta  Alkeisfunktioiden derivaatat [ 1
2 3 ]
Alkeisfunktioiden derivaatat [ 1
2 3 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) derivaatta,
derivaatta, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt
derivointisäännöt
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) potenssi,
potenssi, ![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio,
eksponenttifunktio, ![[#]](kuvat/msam10-c-4.gif) logaritmifunktio,
logaritmifunktio,
![[#]](kuvat/msam10-c-4.gif) trigonometriset funktiot,
trigonometriset funktiot, ![[#]](kuvat/msam10-c-4.gif) arcus-funktiot,
arcus-funktiot, ![[#]](kuvat/msam10-c-4.gif) hyperbelifunktiot,
hyperbelifunktiot, ![[#]](kuvat/msam10-c-4.gif) area-funktiot,
area-funktiot,
![[#]](kuvat/msam10-c-4.gif) integraalifunktio
integraalifunktio
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |