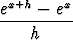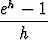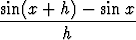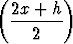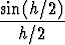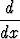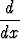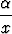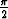Derivaattojen johtamisesta: standardiraja-arvojen
käyttö
Edellä olevien derivaattojen johtaminen perustuu derivaatan määritelmään
erotusosamäärän raja-arvona, funktioiden standardiraja-arvoihin, osamäärän
derivointisääntöön sekä käänteisfunktion derivoimissääntöön. Suoraan
erotusosamäärän raja-arvona ja eräiden standardiraja-arvojen avulla saadaan
eksponenttifunktion ja sinifunktion derivaatat:
limh 0 0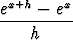 = limh = limh 0ex 0ex 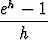 = ex; = ex; |
| |
limh 0 0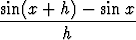 = limh = limh 0 cos 0 cos 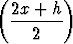 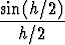 = cos x. = cos x. |
Jälkimmäisessä on käytetty myös sopivaa trigonometrian kaavaa.
Potenssin derivoimiskaava yleisessä tapauksessa, so. eksponentin  ollessa mikä
tahansa reaaliluku, saadaan helpoimmin eksponenttifunktion avulla:
ollessa mikä
tahansa reaaliluku, saadaan helpoimmin eksponenttifunktion avulla:
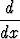 x
x =
= 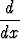 e
e ln x = e
ln x = e ln x
ln x 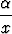 =
=  x
x -1.
-1.
Jos  on kokonaisluku tai rationaaliluku, on muitakin tapoja kaavan
johtamiseen.
on kokonaisluku tai rationaaliluku, on muitakin tapoja kaavan
johtamiseen.
Kosinifunktion derivaatta saadaan palautetuksi edellä johdettuun sinifunktion
derivaattaan kirjoittamalla cos x = sin(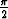 + x). Hyperbelisinin ja hyperbelikosinin
derivaatat voidaan laskea lausumalla funktiot eksponenttifunktion avulla.
+ x). Hyperbelisinin ja hyperbelikosinin
derivaatat voidaan laskea lausumalla funktiot eksponenttifunktion avulla.
Tangentin ja kotangentin sekä vastaavien hypebolisten funktioiden derivaatat
lasketaan lausumalla funktiot sinin ja kosinin, vastaavasti hyperbelisinin
ja hyperbelikosinin avulla ja käyttämällä osamäärän derivoimiskaavaa.
Vaihtoehtoisten muotojen johtamisessa tarvitaan trigonometrian kaavaa
1 = cos2x + sin2x ja tämän hyperbolista vastinetta 1 = cosh2x - sinh2x.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Derivaatta
Derivaatta  Alkeisfunktioiden derivaatat [ 1
2 3 ]
Alkeisfunktioiden derivaatat [ 1
2 3 ]
![[#]](kuvat/msam10-c-4.gif) derivaatta,
derivaatta, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt
derivointisäännöt
![[#]](kuvat/msam10-c-4.gif) potenssi,
potenssi, ![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio,
eksponenttifunktio, ![[#]](kuvat/msam10-c-4.gif) logaritmifunktio,
logaritmifunktio,
![[#]](kuvat/msam10-c-4.gif) trigonometriset funktiot,
trigonometriset funktiot, ![[#]](kuvat/msam10-c-4.gif) arcus-funktiot,
arcus-funktiot, ![[#]](kuvat/msam10-c-4.gif) hyperbelifunktiot,
hyperbelifunktiot, ![[#]](kuvat/msam10-c-4.gif) area-funktiot,
area-funktiot,
![[#]](kuvat/msam10-c-4.gif) integraalifunktio
integraalifunktio
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto